题目内容
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.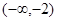 | B.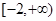 | C.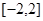 | D.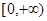 |
B
解析试题分析:根据题意,由于对一切实数x,不等式 恒成立,那么可知
恒成立,那么可知 恒成立,那么可知
恒成立,那么可知
,当|x|=1,时成立,
当x=0时,则a可以取一切实数,
因此可知a的范围是取交集得到为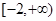 ,故选B.
,故选B.
考点:本试题主要是考查了不等式的恒成立问题的运用。
点评:对于含有参数的不等式的恒成立问题,可以采用分离参数a的思想来得到其取值范围即可。如果直接法用二次函数比较麻烦些。这也是一种很好的等价转化方法之一,属于基础题。

练习册系列答案
相关题目
若不等式x2+ax+1³0对于一切xÎ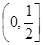 恒成立,则a的最小值是 ( )
恒成立,则a的最小值是 ( )
| A.0 | B.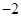 | C.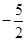 | D.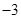 |
设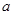 、
、 、
、 是互不相等的正数,现给出下列不等式 ⑴
是互不相等的正数,现给出下列不等式 ⑴ ;⑵
;⑵
 ;⑶
;⑶ ;⑷
;⑷ ,则其中正确个数是( )
,则其中正确个数是( )
| A.0 | B.1 | C.2 | D.3 |
不等式 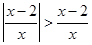 的解集是( )
的解集是( )
A.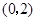 | B.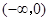 | C.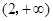 | D.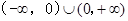 |
当m>1时,关于x的不等式x2+(m-1)x-m≥0的解集是
| A.{x|x≤1,或x≥-m} | B. {x|1≤x≤-m } |
| C.{x|x≤-m,或x≥1} | D. {x|-m≤x≤1 } |
不等式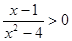 的解集是 ( )
的解集是 ( )
A.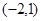 | B.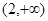 | C.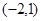  | D.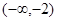 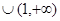 |
设a、b、c都是正数,则 、
、 、
、 三个数 ( )
三个数 ( )
| A.都大于2 | B.都小于2 |
| C.至少有一个大于2 | D.至少有一个不小于2 |
已知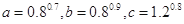 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )
| A.c>a>b | B.b>a>c | C.c>b>a | D.a>b>c |
 的解集是( )
的解集是( )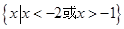 B
B 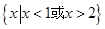
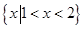 D.
D.