题目内容
不等式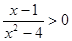 的解集是 ( )
的解集是 ( )
A.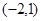 | B.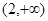 | C.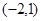  | D.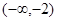 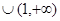 |
C
解析试题分析:由于分式不等式

对于x>1时,则有x>2,当x<1时,则有-2<x<2,故可知不等式的解集为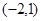
 ,选C.
,选C.
考点:本试题考查了分式不等式的求解。
点评:解决这类问题的关键是要对于已知的不等式化为整式不等式,然后借助于二次不等式的解法得到结论,掌握 的结论,属于基础题。
的结论,属于基础题。

练习册系列答案
相关题目
不等式 的解集为
的解集为
A. | B.[-1,1] | C. | D.[0,1] |
关于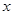 的不等式
的不等式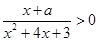 的解为
的解为 或
或 ,则
,则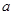 的取值为( )
的取值为( )
| A.2 | B.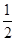 | C.-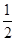 | D.-2 |
若不等式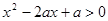 ,对
,对 恒成立,则关于
恒成立,则关于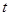 的不等式
的不等式 的解集为 ( )
的解集为 ( )
A. | B.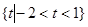 |
C.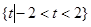 | D. |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.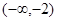 | B.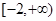 | C.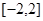 | D.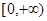 |
不等式 对任意实数
对任意实数 恒成立,则实数
恒成立,则实数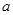 的取值范围为( )
的取值范围为( )
A. | B. |
C.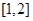 | D. |
若 ,则下列结论不正确的是 ( )
,则下列结论不正确的是 ( )
A. | B. |
C. | D. |
已知 ,则
,则 的取值范围是
的取值范围是
A. | B.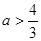 | C. | D. |
不等式 的解集为( )
的解集为( )
| A.(-3,3) | B.(3,+∞) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3) |