题目内容
若不等式x2+ax+1³0对于一切xÎ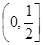 恒成立,则a的最小值是 ( )
恒成立,则a的最小值是 ( )
| A.0 | B.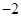 | C.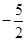 | D.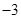 |
C
解析试题分析:将参数a与变量x分离,将不等式恒成立问题转化为求函数最值问题,即可得到结论。解:不等式x2+ax+1≥0对一切x∈(0, ]成立,等价于a≥-x-
]成立,等价于a≥-x- 对于一切x∈(0,
对于一切x∈(0, 〕成立,∵y=-x-
〕成立,∵y=-x- 在区间(0,
在区间(0, 〕上是增函数,∴-x-
〕上是增函数,∴-x- <-
<- -2=-
-2=- ∴a≥-
∴a≥- ∴a的最小值为-
∴a的最小值为- 故答案为C.
故答案为C.
考点:不等式的应用
点评:本题综合考查了不等式的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想,属于中档题

练习册系列答案
相关题目
已知x>0,y>0,若 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )
| A.m≥4或m≤-2 | B.m≥2或m≤-4 |
| C.-2<m<4 | D.-4<m<2 |
若不等式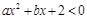 的解集为
的解集为 或
或 ,则
,则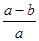 的值为( )
的值为( )
A. | B.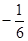 | C.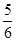 | D. |
不等式 的解集是
的解集是
A. | B. |
C.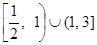 | D. |
要证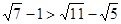 ,只需证
,只需证 ,即需
,即需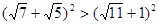 ,即需证
,即需证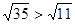 ,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
,即证35>11,因为35>11显然成立,所以原不等式成立。以上证明运用了
| A.比较法 | B.综合法 | C.分析法 | D.反证法 |
不等式 的解集为
的解集为
A. | B.[-1,1] | C. | D.[0,1] |
若 ,则下面四个式子中恒成立的是( )
,则下面四个式子中恒成立的是( )
A. | B. |
C. | D. |
记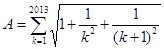 ,再记
,再记 表示不超过A的最大整数,则
表示不超过A的最大整数,则 ( )
( )
| A.2010 | B.2011 | C.2012 | D.2013 |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.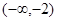 | B.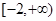 | C.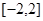 | D.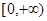 |