题目内容
设a、b、c都是正数,则 、
、 、
、 三个数 ( )
三个数 ( )
| A.都大于2 | B.都小于2 |
| C.至少有一个大于2 | D.至少有一个不小于2 |
D
解析试题分析:∵a,b,c都是正数,
故这三个数的和 ( )+(
)+( )+(
)+( )=a+
)=a+ +b+
+b+ +c+
+c+ ≥2+2+2=6.
≥2+2+2=6.
当且仅当 a=b=c=1时,等号成立.
故三个数中,至少有一个不小于2(否则这三个数的和小于6).
故选D.
考点:本题主要考查用反证法证明不等式,基本不等式的应用。
点评:应用基本不等式,要注意检验等号成立的条件,式子的变形是解题的关键,中档题.

练习册系列答案
相关题目
若 ,则下面四个式子中恒成立的是( )
,则下面四个式子中恒成立的是( )
A. | B. |
C. | D. |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.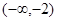 | B.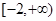 | C.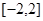 | D.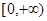 |
不等式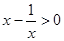 成立的充分不必要条件是( )
成立的充分不必要条件是( )
A.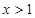 | B.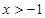 |
C.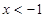 或 或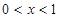 | D.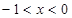 或 或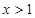 |
若 ,则下列结论不正确的是 ( )
,则下列结论不正确的是 ( )
A. | B. |
C. | D. |
若不等式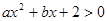 的解集为
的解集为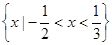 ,则a-b值是( )
,则a-b值是( )
| A.-10 | B.-14 | C.10 | D.14 |
已知不等式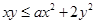 ,若对任意
,若对任意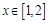 及
及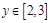 ,该不等式恒成立,则实数
,该不等式恒成立,则实数 的范围是( )
的范围是( )
A.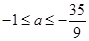  | B.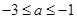 |
C. | D.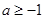 |
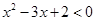 的解集为( )
的解集为( )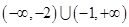 B.
B.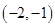
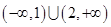 D.
D.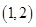
 的解集是_____ ___.
的解集是_____ ___.