题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设![]() 是曲线
是曲线![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线![]() 的斜率
的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() 有两个极值点
有两个极值点![]() 且
且![]() ,若
,若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单增区间为![]() ;单调减区间为
;单调减区间为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)利用题意求解![]() 的解析式,然后求解分式不等式即可得到函数的单调区间;
的解析式,然后求解分式不等式即可得到函数的单调区间;
(2)对导函数分离系数,结合均值不等式的结论讨论实数![]() 的取值范围即可;
的取值范围即可;
(3)利用题意分析所给的问题,构造函数,设设![]() ,
,
讨论函数![]() 的性质即可得到实数
的性质即可得到实数![]() 的取值范围.
的取值范围.
试题解析:
(1)![]() ,
,
令![]() 或
或![]() ,
,
![]() 的单调增区间为
的单调增区间为![]() ;单调减区间为
;单调减区间为![]() .
.
![]() 即
即![]() ,所以
,所以![]() ,
,
令![]() 在
在![]() 上单调递增,
上单调递增,
![]() ∴
∴![]() ,对
,对![]() 恒成立,
恒成立,
![]() ,对
,对![]() 恒成立,
恒成立,
又![]() ,当
,当![]() 时取等号,
时取等号,
![]() ,故
,故![]() .
.
(3)![]() ,因为函数
,因为函数![]() 有两个极值点
有两个极值点![]() ,所以
,所以![]() 是方程
是方程![]() 的两个根,即,所以是
的两个根,即,所以是![]() 方程
方程![]() 的两个根,
的两个根,
所以有![]() ,
,
∴![]()
![]()
![]()
令![]() ,则
,则![]() ,设
,设![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单减,∴
上单减,∴![]() ,
,
故![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中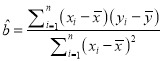 ,
, ![]() )
)