题目内容
已知圆C:x2+y2-2x+4y-4=0,斜率为1的直线l交圆C与A、B两点.
(1)化圆C的方程为标准方程,并指出圆心和半径;
(2)是否存在直线l,使以线段AB为直径的圆过原点?若存在,求出直线l的方程;若不存在,说明理由;
(3)当直线l平行移动时,求△CAB面积的最大值.
(1)化圆C的方程为标准方程,并指出圆心和半径;
(2)是否存在直线l,使以线段AB为直径的圆过原点?若存在,求出直线l的方程;若不存在,说明理由;
(3)当直线l平行移动时,求△CAB面积的最大值.
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(1)利用配方法,化圆C的方程为标准方程,可得圆心与半径;
(2)假设所求直线存在,将条件以AB为直径的圆经过原点O,转化为OA⊥OB.通过联立方程可求;
(3)求出△CAB面积,即可求出最大值.
(2)假设所求直线存在,将条件以AB为直径的圆经过原点O,转化为OA⊥OB.通过联立方程可求;
(3)求出△CAB面积,即可求出最大值.
解答:
解:(1)圆C化成标准方程为:(x-1)2+(y+2)2=32,
∴圆心为C(1,-2),半径r=3. …(2分)
(2)设以线段AB为直径的圆为M,且圆心M的坐标为(a,b).
由于CM⊥l,∴kCM•kl=-1,即
×1=-1,
∴a+b+1=0,①…(3分)
由于直线l过点M(a,b),∴l的方程可写为y-b=x-a,即x-y+b-a=0,
因此|CM|=
. …(4分)
又∵以AB为直径的圆M过原点,∴|MA|=|MB|=|OM|. …(5分)
而|MB|2=|CB|2-|CM|2=9-(
)2,|OM|2=a2+b2
所以9-(
)2=a2+b2②…(6分)
由①②得:a=
或a=-1.
当a=
时,b=-
,此时直线l的方程为x-y-4=0;
当a=-1时,b=0,此时直线l的方程为x-y+1=0.
∴所求斜率为1的直线l是存在的,其方程为x-y-4=0或x-y+1=0.…(8分)
(3)设AB的中点为M,则|AB|=2|MB|=2
,|CM|=
,
∴S△CAB=
|AB||CM|=
≤
,
当
或
时等号成立,此时直线L的方程为x-y=0或x-y-6=0,满足题意,△CAB面积的最大值为
.
∴圆心为C(1,-2),半径r=3. …(2分)
(2)设以线段AB为直径的圆为M,且圆心M的坐标为(a,b).
由于CM⊥l,∴kCM•kl=-1,即
| b+2 |
| a-1 |
∴a+b+1=0,①…(3分)
由于直线l过点M(a,b),∴l的方程可写为y-b=x-a,即x-y+b-a=0,
因此|CM|=
| |b-a+3| | ||
|
又∵以AB为直径的圆M过原点,∴|MA|=|MB|=|OM|. …(5分)
而|MB|2=|CB|2-|CM|2=9-(
| |b-a+3| | ||
|
所以9-(
| |b-a+3| | ||
|
由①②得:a=
| 3 |
| 2 |
当a=
| 3 |
| 2 |
| 5 |
| 2 |
当a=-1时,b=0,此时直线l的方程为x-y+1=0.
∴所求斜率为1的直线l是存在的,其方程为x-y-4=0或x-y+1=0.…(8分)
(3)设AB的中点为M,则|AB|=2|MB|=2
| 9-|CM|2 |
| |2-2a| | ||
|
∴S△CAB=
| 1 |
| 2 |
-2[2(a-1)2-
|
| 9 |
| 2 |
当
|
|
| 9 |
| 2 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
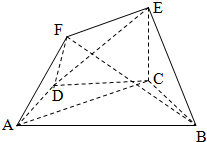 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=