题目内容
数列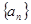 满足
满足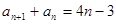
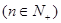 .
.
(Ⅰ)若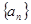 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若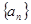 满足
满足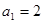 ,
,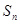 为
为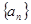 的前
的前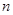 项和,求
项和,求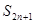 .
.
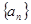 满足
满足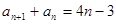
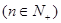 .
.(Ⅰ)若
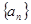 是等差数列,求其通项公式;
是等差数列,求其通项公式;(Ⅱ)若
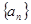 满足
满足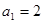 ,
,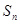 为
为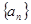 的前
的前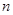 项和,求
项和,求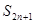 .
. 解:(I)
(Ⅱ) =
=

(Ⅱ)
 =
=
本试题主要是考查了运用数列的递推关系,求解数列的通项公式,以及结合等差数列的通项公式求解,并求解数列的和。
(1)根据题意,联立两个递推关系式,然后做差得到结论。
(2)根据首项为2,那么我们可以分析奇数项与偶数项分别构成等差数列,公差均为4,然后累加法得到结论。
(1)根据题意,联立两个递推关系式,然后做差得到结论。
(2)根据首项为2,那么我们可以分析奇数项与偶数项分别构成等差数列,公差均为4,然后累加法得到结论。

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
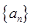 是公差不为零的等差数列,
是公差不为零的等差数列,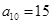 ,且
,且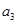 、
、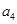 、
、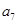 成等比数列.
成等比数列. 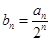 ,数列
,数列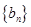 的前
的前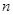 项和为
项和为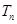 ,求证:
,求证: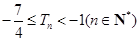
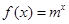 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).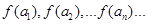 (n∈
(n∈ ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.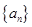 是等差数列;
是等差数列; 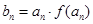 ,且数列
,且数列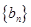 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;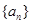 的前
的前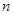 项和为
项和为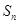 ,则
,则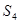 ,
,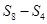 ,
,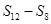 ,
,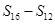 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列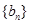 的前
的前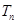 ,则
,则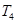 ,______,________
,______,________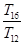 成等比数列.
成等比数列.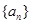 的前n项和为
的前n项和为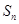 ,点
,点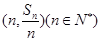 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.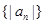 的前n项的和.
的前n项的和.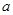 所代表的正整数是
所代表的正整数是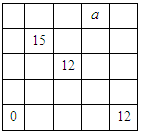
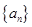 的首项为
的首项为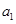 ,公差
,公差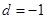 ,前
,前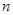 项和为
项和为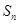
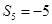 ,求
,求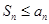 对任意正整数
对任意正整数 的前100项和为( )
的前100项和为( )



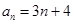 ,则数列{an}是公差为 的等差数列.
,则数列{an}是公差为 的等差数列.