题目内容
(本小题满分14分)
已知数列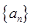 是公差不为零的等差数列,
是公差不为零的等差数列,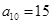 ,且
,且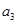 、
、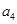 、
、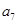 成等比数列.
成等比数列.
(Ⅰ)求数列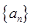 的通项公式;
的通项公式;
(Ⅱ)设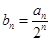 ,数列
,数列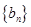 的前
的前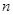 项和为
项和为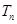 ,求证:
,求证: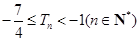
已知数列
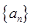 是公差不为零的等差数列,
是公差不为零的等差数列,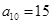 ,且
,且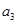 、
、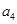 、
、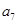 成等比数列.
成等比数列. (Ⅰ)求数列
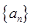 的通项公式;
的通项公式;(Ⅱ)设
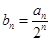 ,数列
,数列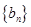 的前
的前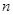 项和为
项和为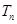 ,求证:
,求证: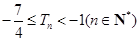
(Ⅰ)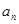
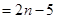 ,(
,(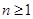 );(Ⅱ)证明: 见解析。
);(Ⅱ)证明: 见解析。
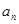
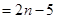 ,(
,(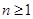 );(Ⅱ)证明: 见解析。
);(Ⅱ)证明: 见解析。本试题主要是考查了等差数列的通项公式以及数列的求和的综合运用。
(1)根据已知中设数列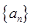 的公差为
的公差为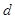 (
(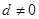 ),由已知得:
),由已知得:
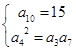 联立方程组得到结论。
联立方程组得到结论。
(2)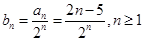 那么利用错位相减法得到求和。
那么利用错位相减法得到求和。
(Ⅰ) 解:设数列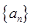 的公差为
的公差为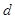 (
(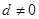 ),由已知得:
),由已知得:
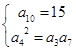 即:
即: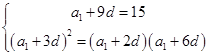 ------2分
------2分
解之得: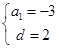 --------------4分
--------------4分
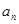
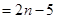 ,(
,(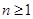 ) ---------------6分
) ---------------6分
(Ⅱ)证明: ∵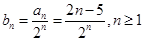 .
.
 , ①
, ①
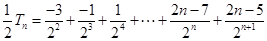 . ②
. ②
①-②得:
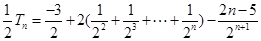
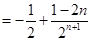
得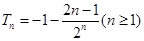 , ----------10分
, ----------10分
∵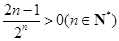 ,
,
∴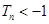 . ------------------12分
. ------------------12分
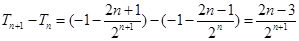 ,
,
∴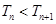 .
. 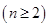 -----------14分
-----------14分
(1)根据已知中设数列
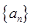 的公差为
的公差为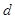 (
(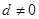 ),由已知得:
),由已知得: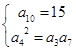 联立方程组得到结论。
联立方程组得到结论。(2)
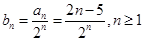 那么利用错位相减法得到求和。
那么利用错位相减法得到求和。(Ⅰ) 解:设数列
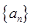 的公差为
的公差为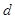 (
(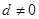 ),由已知得:
),由已知得: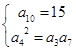 即:
即: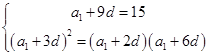 ------2分
------2分解之得:
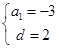 --------------4分
--------------4分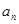
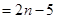 ,(
,(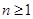 ) ---------------6分
) ---------------6分(Ⅱ)证明: ∵
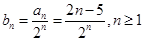 .
.  , ①
, ①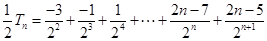 . ②
. ②①-②得:
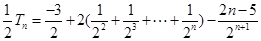
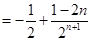
得
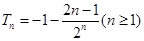 , ----------10分
, ----------10分∵
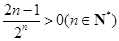 ,
,∴
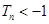 . ------------------12分
. ------------------12分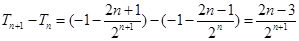 ,
,∴
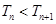 .
. 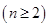 -----------14分
-----------14分
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
, (
(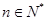 ).
). 是等比数列,求出数列
是等比数列,求出数列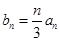 ,求数列
,求数列 的前
的前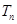 ;
;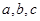 成等比数列,
成等比数列,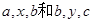 分别成等差数列,且
分别成等差数列,且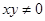 ,则
,则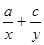 的值等于( )
的值等于( )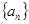 的前n项和
的前n项和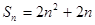 ,数列
,数列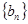 的前n项和
的前n项和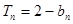 ,
,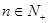 ,
,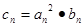 ,是否存在正整数
,是否存在正整数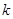 ,使得
,使得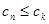 对
对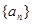 为等差数列,若
为等差数列,若 ,且它的前
,且它的前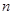 项和
项和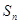 有最小值,那么当
有最小值,那么当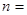
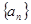 满足
满足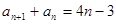
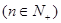 .
.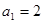 ,
,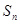 为
为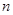 项和,求
项和,求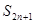 .
. 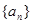 ,
,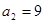 ,
,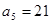 ,
,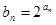 ,求数列
,求数列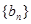 的前
的前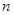 项和
项和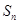 。
。  中,
中,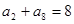 ,则该数列前9项和
,则该数列前9项和
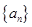 中,
中,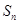 是其前n项和,
是其前n项和,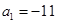 ,
,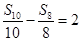 则
则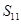 =( )
=( )