题目内容
已知直线 交于A,B两点,且
交于A,B两点,且 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
A. 2 2 | B. |
C. 1 1 | D.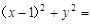 4 4 |
B
解析试题分析:联立直线方程与抛物线方程并整理得 ,
,
设 则
则
因为 ,所以
,所以 ,所以
,所以 ,代入数据可得
,代入数据可得 ,所以直线
,所以直线 ,所以直线恒过定点(2,0),
,所以直线恒过定点(2,0),
因为OM⊥AB,所以 ,整理得
,整理得 即为点M的轨迹方程.
即为点M的轨迹方程.
考点:本小题主要考查直线与抛物线的性质,向量的运算,直线过定点,轨迹问题.
点评:解决本小题的关键是根据 可得
可得 ,从而利用韦达定理知道
,从而利用韦达定理知道 ,本小题运算量比较大,要仔细运算,另外要注意直线过定点问题.
,本小题运算量比较大,要仔细运算,另外要注意直线过定点问题.

练习册系列答案
相关题目
直线 过点
过点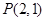 与曲线
与曲线 恰有一个公共点,则满足条件的直线
恰有一个公共点,则满足条件的直线 的条数为( )
的条数为( )
| A.1 | B.2 | C.3 | D.4 |
斜率为 的直线与双曲线
的直线与双曲线 (a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
(a>0,b>0)恒有两个公共点,则双曲线离心率的取值范围是
A. | B. | C. | D. |
到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )。
| A.直线 | B.椭圆 | C.抛物线 | D.双曲线 |
椭圆 的两焦点之间的距离为
的两焦点之间的距离为
A. | B. | C. | D. |
如图,用与底面成 角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
角的平面截圆柱得一椭圆截线,则该椭圆的离心率为 ( )
A. | B. | C. | D.非上述结论 |
双曲线 的渐近线方程为
的渐近线方程为
A.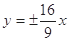 | B. | C. | D. |
已知函数 是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
是偶函数,则函数的图象与y轴交点的纵坐标的最大值为:( )
| A.-4 | B.2 | C.3 | D.4 |
 右支上一点,
右支上一点, 分别为双曲线的左、右焦点,I为△
分别为双曲线的左、右焦点,I为△ 的内心,若
的内心,若 成立,则
成立,则 的值为( )
的值为( )


