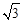题目内容
直线 过点
过点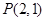 与曲线
与曲线 恰有一个公共点,则满足条件的直线
恰有一个公共点,则满足条件的直线 的条数为( )
的条数为( )
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:根据题意,直线 过点
过点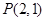 与曲线
与曲线 恰有一个公共点,而又因为点
恰有一个公共点,而又因为点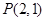 在渐近线上,故旋转直线一周只有两条符合条件,故选B.
在渐近线上,故旋转直线一周只有两条符合条件,故选B.
考点:直线与双曲线的位置关系
点评:解决的关键是利用直线与双曲线有一个公共点的情况可能相切,也可能平行于其渐近线得到,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线 与双曲线
与双曲线 的右支交于不同的两点,那么
的右支交于不同的两点,那么 的取值范围是( )
的取值范围是( )
A.( ) ) | B.( ) ) |
C.( ) ) | D.( ) ) |
经过点 ,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
,并且对称轴都在坐标轴上的等轴双曲线的方程为( )
A. | B. |
C. 或 或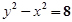 | D. |
若方程C: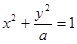 (
(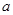 是常数)则下列结论正确的是( )
是常数)则下列结论正确的是( )
A. ,方程C表示椭圆 ,方程C表示椭圆 | B. ,方程C表示双曲线 ,方程C表示双曲线 |
C.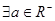 ,方程C表示椭圆 ,方程C表示椭圆 | D.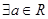 ,方程C表示抛物线 ,方程C表示抛物线 |
椭圆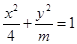 的焦距为2,则
的焦距为2,则 的值为( )
的值为( )
| A.3 | B. | C.3或5 | D.3或 |
抛物线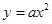 的准线方程为
的准线方程为 ,则实数
,则实数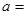 ( )
( )
| A.4 | B.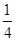 | C.2 | D. |
直线 与曲线
与曲线 相切于点
相切于点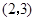 ,则
,则 的值为 ( )
的值为 ( )
| A.5 | B. 6 | C. 4 | D. 9 |
已知直线 交于A,B两点,且
交于A,B两点,且 (其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
(其中O为坐标原点),若OM⊥AB于M,则点M的轨迹方程为 ( )
A. 2 2 | B. |
C. 1 1 | D.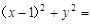 4 4 |
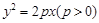 的焦点为
的焦点为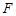 ,点
,点 在此抛物线上,且
在此抛物线上,且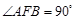 ,弦
,弦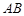 的中点
的中点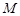 在该抛物线准线上的射影为
在该抛物线准线上的射影为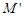 ,则
,则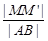 的最大值为( )
的最大值为( )