题目内容
若函数y=sin（2x+?）的一条对称轴为
，则它的一个单调区间为
- A.
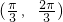
- B.
- C.
- D.
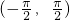
A
分析：利用正弦函数的对称轴方程2x+φ=kπ+
，k∈Z即可求得φ，再利用正弦函数的单调性即可求得答案．
解答：∵x=
是函数y=sin（2x+?）的一条对称轴，
∴2×+φ=kπ+，
不妨取k=0，φ=-
，
由2kπ+≤2x-≤2kπ+
，k∈Z，得
kπ+≤x≤kπ+
，k∈Z，
令k=0，≤x≤，
∴y=sin（2x-）的一个单调递减区间为[，]，而（，）?[，]，故A正确，可排除B，C，D．
故选A．
点评：本题考查正弦函数的对称性与单调性，求得φ是关键，考查分析与推理运算能力，属于中档题．
分析：利用正弦函数的对称轴方程2x+φ=kπ+
，k∈Z即可求得φ，再利用正弦函数的单调性即可求得答案．解答：∵x=
是函数y=sin（2x+?）的一条对称轴，∴2×
+φ=kπ+，不妨取k=0，φ=-
，由2kπ+
≤2x-≤2kπ+，k∈Z，得kπ+
≤x≤kπ+，k∈Z，令k=0，
≤x≤，∴y=sin（2x-
）的一个单调递减区间为[，]，而（，）?[，]，故A正确，可排除B，C，D．故选A．
点评：本题考查正弦函数的对称性与单调性，求得φ是关键，考查分析与推理运算能力，属于中档题．
练习册系列答案
相关题目
若函数