题目内容
3.已知复数z1=cosα+isinα,z2=cosβ+isinβ,则复数z1•z2的实部是cos(α+β).分析 利用多项式乘多项式展开,结合两角和与差的正弦、余弦化简得答案.
解答 解:∵z1=cosα+isinα,z2=cosβ+isinβ,
∴z1•z2=(cosα+isinα)(cosβ+isinβ)
=cosαcosβ-sinαsinβ+(cosαsinβ+sinαcosβ)i
=cos(α+β)+sin(α+β)i.
∴z1•z2的实部为cos(α+β).
故答案为:cos(α+β).
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
13.阅读如图的程序框图,则输出的S等于( )
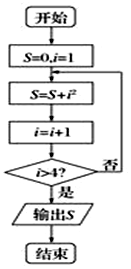

| A. | 55 | B. | 30 | C. | 20 | D. | 10 |
14.抛物线x2=-6by的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右支分别交于B、C两点,A为双曲线的右顶点,O为坐标原点,若∠AOC=∠BOC,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 3 | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
18.若f(x)=$\frac{e^x}{x}$,f'(x)为f(x)的导函数,则f'(x)=( )
| A. | f'(x)=$-\frac{e^x}{x}$ | B. | f'(x)=$\frac{{x{e^x}-{e^x}}}{x^2}$ | C. | f'(x)=$\frac{{x{e^x}+{e^x}}}{x^2}$ | D. | f'(x)=$\frac{{x{e^x}-{e^x}}}{x}$ |
12.假设行列式的计算公式:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,若f(x)=$|\begin{array}{l}{x}&{x}\\{3}&{{x}^{2}}\end{array}|$,则函数f(x)的单调减区间为( )
| A. | $(-\sqrt{3},\sqrt{3})$ | B. | (-1,1) | C. | $(-\sqrt{2},\sqrt{2})$ | D. | (-2,2) |