题目内容
14.在△ABC中,C=90°,CB=3,点M是AB上的动点(包含端点),则$\overrightarrow{MC}$•$\overrightarrow{CB}$的取值范围为[-9,0].分析 以C为坐标原点,CB,CA所在直线为x,y轴建立直角坐标系,表示出点C、B、A,设出点M的坐标,求出$\overrightarrow{MC}$•$\overrightarrow{CB}$的取值范围.
解答 解:如图所示,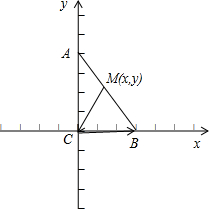
以C为坐标原点,CB,CA所在直线为x,y轴建立直角坐标系,
则C(0,0),B(3,0),A(0,a),其中a>0;
设M(x,y),其中0≤x≤3,
则$\overrightarrow{MC}$=(-x,-y),$\overrightarrow{CB}$=(3,0),
∴$\overrightarrow{MC}$•$\overrightarrow{CB}$=-3x;
由于0≤x≤3,
∴-9≤-3x≤0,
∴$\overrightarrow{MC}$•$\overrightarrow{CB}$的取值范围是[-9,0].
故答案为:[-9,0].
点评 本题考查了平面向量数量积的坐标表示以及应用问题,也考查了函数的最值问题,是基础题目.

练习册系列答案
相关题目
19.已知y=f(x)为(0,+∞)上的可导函数,且(x+1)f′(x)>f(x),则以下一定成立的是( )
| A. | 3f(4)<4f(3) | B. | 3f(4)>4f(3) | C. | 3f(3)<4f(2) | D. | 3f(3)>4f(2) |
 如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.
如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA. 在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.
在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.