题目内容
已知中心在原点,焦点在x轴上的椭圆的左顶点为A,上顶点为B,左焦点F到直线AB的距离为
|OB|,求椭圆的离心率.
e=
解析:
解法一:直线AB的方程为
+
=1,即bx-ay+ab=0,
∴d=
=b.
∵a2-b2=c2,a>b,a>c,
∴5a2-14ac+8c2=0.
∴8e2-14e+5=0.
解得e=或e=
(舍).
解法二:如图,作F1D⊥AB于D,则|F1D|=|OB|=b.
由△AF1D∽△ABO,得
.
∴5a2-14ac+8c2=0.
∴8e2-14e+5=0.解得e=或e=(舍).
练习册系列答案
相关题目
|OB|,求椭圆的离心率.
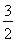
,且经过点
,过椭圆的左焦点作直线
交椭圆于A、B两点，以OA、OB为邻边作平行四边形OAPB。
,且椭圆经过点
，
与椭圆C交于不同的两点A,B满足
·
,若存在,求出直线