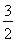Question

已知中心在原点,焦点在x轴上的椭圆离心率为,且经过点,过椭圆的左焦点作直线交椭圆于A、B两点，以OA、OB为邻边作平行四边形OAPB。 

（1）求椭圆E的方程

（2）现将椭圆E上的点的纵坐标保持不变，横坐标变为原来的一半，求所得曲线的焦点坐标和离心率

（3）是否存在直线，使得四边形OAPB为矩形？若存在，求出直线的方程。若不存在，说明理由。

 

Answer 1

【答案】

（1）；（2）焦点为（0，）,离心率；

（3）或.

【解析】本试主要考查了椭圆的方程和直线与椭圆位置关系的 运用。

解：(1)设椭圆E的方程，由条件得解得，椭圆E的方程……………4分

（2）由题意，变换后的曲线的方程为，所以焦点为（0，）,离心率……………7分

（3）当轴时，A(，2)，B(，-2)，此时不满足；

当AB与x轴不垂直时，设直线AB的斜率是k，且直线过左焦点C(，0)，则直线方程是。

根据题意有，设则=0。

联立方程 得

，，

==0

得，经检验满足

所以存在直线AB满足条件，直线AB的方程是或。……16分