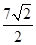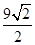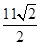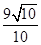题目内容
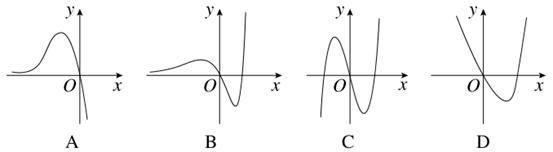
下列关于函数 的性质叙述错误的是( )
的性质叙述错误的是( )
A. 在区间 在区间 上单调递减 上单调递减 |
B. 在定义域上没有最大值 在定义域上没有最大值 |
C. 在 在 处取最大值3 处取最大值3 |
D. 的图像在点 的图像在点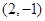 处的切线方程为 处的切线方程为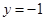 |
C
解析试题分析:因为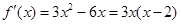 ,于是可得
,于是可得
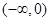

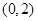
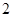
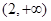
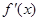
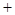
0 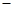
0 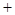


极大值3 
极小值 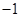

当 时,
时,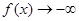 ,当
,当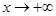 时,
时,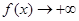
所以可知A、B正确,C不正确, 在
在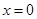 处取得极大值3,并不是最大值
处取得极大值3,并不是最大值
而 的图像在点
的图像在点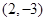 处的切线的斜率为
处的切线的斜率为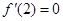 ,故此时的切线方程为
,故此时的切线方程为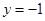
综上可知,只有C是错误的,故选C.
考点:导数在研究函数性质上的应用.

练习册系列答案
相关题目
设函数 是定义在
是定义在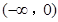 上的可导函数,其导函数为
上的可导函数,其导函数为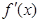 ,且有
,且有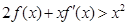 ,则不等式
,则不等式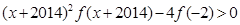 的解集为( )
的解集为( )
A.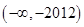 | B.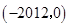 | C.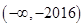 | D.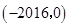 |
若函数 在R上可导,且
在R上可导,且 ,则( )
,则( )
A. | B. | C. | D.无法确定 |
函数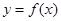 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
A.若函数在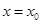 时取得极值,则 时取得极值,则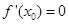 |
B.若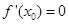 ,则函数在 ,则函数在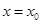 处取得极值 处取得极值 |
C.若在定义域内恒有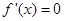 ,则 ,则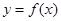 是常数函数 是常数函数 |
D.函数 在 在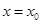 处的导数是一个常数 处的导数是一个常数 |
若函数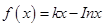 在区间
在区间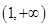 单调递增,则
单调递增,则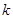 的取值范围是( )
的取值范围是( )
A.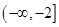 | B.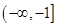 | C.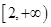 | D.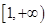 |
设函数 ,
, .若当
.若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数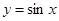 在点
在点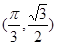 处的切线的斜率为( )
处的切线的斜率为( )
A.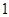 | B.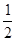 | C.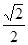 | D.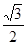 |
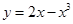 在横坐标为
在横坐标为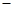 l的点处的切线为
l的点处的切线为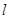 ,则点P(3,2)到直线
,则点P(3,2)到直线