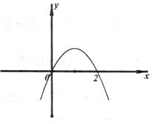
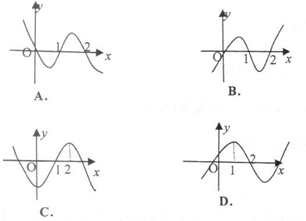
题目内容
设函数 ,
, .若当
.若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析: ,
,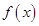 单调递增,又
单调递增,又 为奇函数,原不等式可化为
为奇函数,原不等式可化为 ,即
,即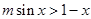 ,可变为
,可变为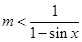 ,又
,又 ,得
,得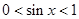 ,
,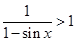 ,所以
,所以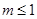 时恒成立.
时恒成立.
考点:利用导数判断函数的单调性,函数的奇偶性,不等式恒成立.

练习册系列答案
相关题目
曲线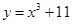 在点
在点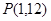 处的切线与
处的切线与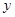 轴交点的纵坐标是( )
轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
函数 的极大值为
的极大值为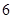 ,那么
,那么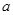 的值是( )
的值是( )
A.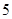 | B. | C.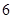 | D.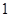 |
下列关于函数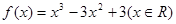 的性质叙述错误的是( )
的性质叙述错误的是( )
A. 在区间 在区间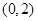 上单调递减 上单调递减 |
B. 在定义域上没有最大值 在定义域上没有最大值 |
C. 在 在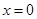 处取最大值3 处取最大值3 |
D. 的图像在点 的图像在点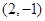 处的切线方程为 处的切线方程为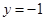 |
要做一个圆锥形的漏斗,其母线长为 ,要使其体积为最大,则高为( )
,要使其体积为最大,则高为( )
A. | B. | C. | D. |
已知函数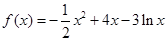 在
在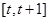 上不单调,则
上不单调,则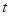 的取值范围是( )
的取值范围是( )
A. | B.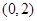 | C. | D. |
函数 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<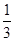 ,则f(x)<
,则f(x)< +
+ 的解集为( )
的解集为( )
| A.{x|-1<x<1} | B.{x|x<-1} |
| C.{x|x<-1或x>1} | D.{x|x>1} |
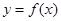 的导函数
的导函数 的图像如图所示,则
的图像如图所示,则