题目内容
函数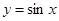 在点
在点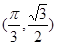 处的切线的斜率为( )
处的切线的斜率为( )
A.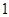 | B.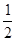 | C.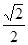 | D.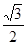 |
B
解析试题分析::令 ,则
,则 ,所以
,所以 。由导数的几何意义可知在点
。由导数的几何意义可知在点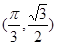 处的切线的斜率
处的切线的斜率 。故B正确。
。故B正确。
考点:导数的几何意义。

练习册系列答案
相关题目
下列关于函数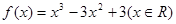 的性质叙述错误的是( )
的性质叙述错误的是( )
A. 在区间 在区间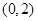 上单调递减 上单调递减 |
B. 在定义域上没有最大值 在定义域上没有最大值 |
C. 在 在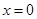 处取最大值3 处取最大值3 |
D. 的图像在点 的图像在点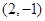 处的切线方程为 处的切线方程为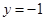 |
若函数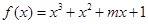 是R上的单调函数,则实数m的取值范围是( )。
是R上的单调函数,则实数m的取值范围是( )。
A. | B. | C. | D.  |
定义在R上的可导函数 f(x)=x2 + 2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,
则m的取值范围是( )
| A.m≥2 | B.2≤m≤4 | C.m≥4 | D.4≤m≤8 |
函数 的单调递减区间为( ).
的单调递减区间为( ).
A. | B. | C. | D. |
函数 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若 ,其中
,其中 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<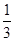 ,则f(x)<
,则f(x)< +
+ 的解集为( )
的解集为( )
| A.{x|-1<x<1} | B.{x|x<-1} |
| C.{x|x<-1或x>1} | D.{x|x>1} |
已知定义在R上的函数f(x),其导函数f′(x)的大致图象如图所示,则下列叙述正确的是( )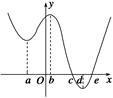
| A.f(b)>f(c)>f(d) |
| B.f(b)>f(a)>f(e) |
| C.f(c)>f(b)>f(a) |
| D.f(c)>f(e)>f(d) |