题目内容
7.(1)利用“五点法”画出函数$f(x)=sin(\frac{1}{2}x+\frac{π}{6})$在$[{-\frac{π}{3},\frac{11π}{3}}]$内的简图| x | |||||
| $\frac{1}{2}$x+$\frac{π}{6}$ | |||||
| y |
(2)若对任意x∈[0,2π],都有f(x)-3<m<f(x)+3恒成立,求m的取值范围.
分析 (1)根据列表、描点、连线的基本步骤,画出函数在一个周期在$[{-\frac{π}{3},\frac{11π}{3}}]$的大致图象即可.
(2)根据x∈[0,2π],求解f(x)的值域,要使f(x)-3<m<f(x)+3恒成立,转化为最小和最大值问题.
解答 解:(1)根据题意,函数$f(x)=sin(\frac{1}{2}x+\frac{π}{6})$在$[{-\frac{π}{3},\frac{11π}{3}}]$内的列表如下:
| x | $-\frac{π}{3}$ | $\frac{2π}{3}$ | $\frac{5π}{3}$ | $\frac{8π}{3}$ | $\frac{11π}{3}$ |
| $\frac{1}{2}x+\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 0 | 1 | 0 | -1 | 0 |
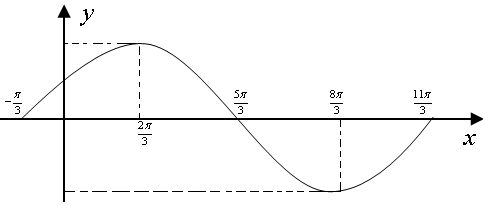
(2)通过图象可知:当x∈[0,2π]时,函f(x)值域为$[{-\frac{1}{2},1}]$,
要使f(x)-3<m<f(x)+3恒成立,
即:$\left\{\begin{array}{l}{1-3<m}\\{-\frac{1}{2}+3>m}\end{array}\right.$
解得:$-2<m<\frac{5}{2}$,
∴m的取值范围是$m∈[{-2,\frac{5}{2}}]$.
点评 本题考查了三角函数的图象与性质的应用问题,解题时应根据画三角函数的图象的基本步骤画出图形,是基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
18.已知椭圆的焦点在y轴上,长轴长为10,短轴长为8,F1、F2为椭圆的左、右焦点.
(1)求椭圆的标准方程;
(2)求椭圆的焦点坐标、离心率;
(3)求以椭圆的焦点为顶点、顶点为焦点的双曲线的标准方程.
(1)求椭圆的标准方程;
(2)求椭圆的焦点坐标、离心率;
(3)求以椭圆的焦点为顶点、顶点为焦点的双曲线的标准方程.
15.已知集合$M=\left\{{\left.{({x,y})}\right|\left\{\begin{array}{l}2x+y=2\\ x-y=1\end{array}\right.}\right\}$,则( )
| A. | M={1,0} | B. | M={(1,0)} | C. | M=(1,0) | D. | M={1} |
17.已知等差数列{an}中,a5=9,且2a3-a2=6,则a1等于( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
 为了测算如图阴影部分的面积,作一个边长为3的正方形将其包含在内,并向正方形内随机投掷600个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )
为了测算如图阴影部分的面积,作一个边长为3的正方形将其包含在内,并向正方形内随机投掷600个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是( )