题目内容
【题目】已知![]() .
.
(1)若函数![]() 是
是![]() 上的增函数,求
上的增函数,求![]() 的取值范围;
的取值范围;
(2)若![]() ,求
,求![]() 的单调增区间.
的单调增区间.
【答案】(1)![]() (2)答案不唯一,见解析
(2)答案不唯一,见解析
【解析】
(1)由函数![]() 是
是![]() 上的增函数,可得
上的增函数,可得![]() 在
在![]() 上恒成立,分离参数可得:
上恒成立,分离参数可得:![]() ,令
,令![]() ,求出
,求出![]() 最小值即可得解;
最小值即可得解;
(2)由![]() ,求导后分
,求导后分![]() ,
,![]() 和
和![]() 三种情况进行讨论即可得解.
三种情况进行讨论即可得解.
解:(1)![]() ,
,
∵![]() 是
是![]() 上的增函数,故
上的增函数,故![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
令![]()
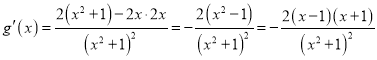
由![]() ,得
,得![]() 或
或![]()
![]() ,得
,得![]() ,
,
![]() ,得
,得![]() 或
或![]() ,
,
故函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单词递增,
上单词递增,
在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时,![]() 有极小值
有极小值![]() ,当
,当![]() 时,
时,![]() 有极大值
有极大值![]() .
.
又∵![]() ,∴
,∴![]() ,
,
故![]() 为函数
为函数![]() 的最小值.
的最小值.
∴![]() ,但当
,但当![]() 时,
时,![]() 亦是
亦是![]() 上的增函数,
上的增函数,
故知![]() 的取值范围是
的取值范围是![]() .
.
(2)![]()
由![]() ,得
,得![]() ,
,
由判别式![]() 可知
可知
①当![]() 时,
时,![]() ,即函数
,即函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,有
时,有![]() ,
,![]() ,
,
即函数![]() 在
在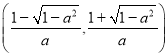 上单调递增;
上单调递增;
③当![]() 时,有
时,有![]() ,
,![]() 或
或![]() ,
,
即函数![]() 在
在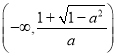 、
、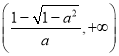 上单调递增.
上单调递增.

练习册系列答案
相关题目
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() ,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度关于声音能量的回归方程.
参考公式: ;
;![]()
【题目】某家庭为了解冬季用电量![]() (度)与气温
(度)与气温![]() 之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
之间的关系,随机统计了某5天的用电量与当天气温,并制作了对照表,经过统计分析,发现气温在一定范围内时,用电量与气温具有线性相关关系:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出用电量![]() 关于气温
关于气温![]() 的线性回归方程;
的线性回归方程;
(2)在这5天中随机抽取两天,求至少有一天用电量低于10(度)的概率.
(附:回归直线方程的斜率和截距的最小二乘法估计公式为 ,
,![]() )
)
