题目内容
定义函数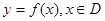 (
( 为定义域)图像上的点到坐标原点的距离为函数的
为定义域)图像上的点到坐标原点的距离为函数的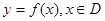 的模.若模存在最大值,则称之为函数
的模.若模存在最大值,则称之为函数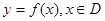 的长距;若模存在最小值,则称之为函数
的长距;若模存在最小值,则称之为函数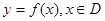 的短距.
的短距.
(1)分别判断函数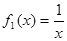 与
与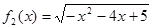 是否存在长距与短距,若存在,请求出;
是否存在长距与短距,若存在,请求出;
(2)求证:指数函数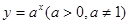 的短距小于1;
的短距小于1;
(3)对于任意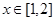 是否存在实数
是否存在实数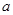 ,使得函数
,使得函数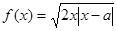 的短距不小于2且长距不大于4.若存在,请求出
的短距不小于2且长距不大于4.若存在,请求出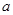 的取值范围;不存在,则说明理由?
的取值范围;不存在,则说明理由?
(1)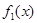 短距为
短距为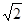 ,长距不存在,
,长距不存在,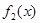 短距为
短距为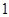 ,长距为5;(2)证明见解析;(3)
,长距为5;(2)证明见解析;(3)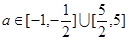 .
.
解析试题分析:本题属于新定义概念,问题的实质是求函数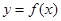 图象上的点到原点的距离的最大值和最小值(如有的话),正面讨论时我们把距离表示为
图象上的点到原点的距离的最大值和最小值(如有的话),正面讨论时我们把距离表示为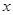 的函数.(1)对
的函数.(1)对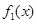 ,
,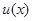
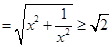 (当且仅当
(当且仅当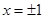 时等号成立),因此存在短距为
时等号成立),因此存在短距为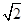 ,不存在长距,对
,不存在长距,对 ,
,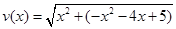
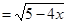 ,
,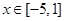 ,即有最大值也有最小值,因此短距和长距都有;(2)对函数
,即有最大值也有最小值,因此短距和长距都有;(2)对函数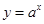 ,
,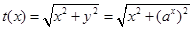 ,由于
,由于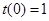 ,因此短距不大于1,令
,因此短距不大于1,令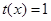 ,则有
,则有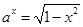 ,故当
,故当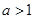 时,存在
时,存在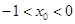 使得
使得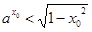
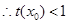 ,当
,当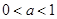 时,存在
时,存在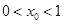 使得
使得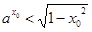
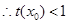 ,即证;(3)记
,即证;(3)记 ,按题意条件,则有不等式
,按题意条件,则有不等式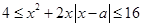 对
对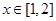 恒成立,这类不等式恒成立求参数取值范围问题,我们可采取分离参数法,转化为求函数的最值,对
恒成立,这类不等式恒成立求参数取值范围问题,我们可采取分离参数法,转化为求函数的最值,对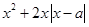
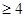 ,
,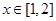 ,按
,按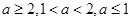 分别讨论,对
分别讨论,对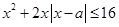 ,
,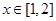 ,可得
,可得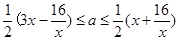 ,由此可求得
,由此可求得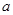 的范围.
的范围.
试题解析:(1)设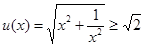 (当且仅当
(当且仅当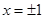 取得等号)
取得等号)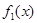 短距为
短距为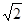 ,长距不存在. +2分
,长距不存在. +2分
设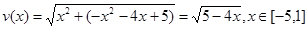 +3分
+3分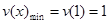
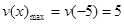
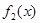 短距为
短距为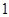 ,长距为5. +5分
,长距为5. +5分
(2)设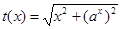
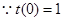
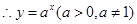 的短距不大于1 +7分
的短距不大于1 +7分
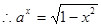
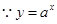 与单位圆存在两个交点
与单位圆存在两个交点
当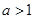 时,存在
时,存在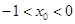 使得
使得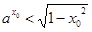
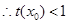
当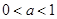 时,存在
时,存在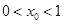 使得
使得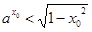
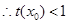
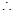 指数函数
指数函数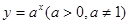 的短距小于1; +10分
的短距小于1; +10分
(3)设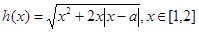
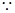 函数
函数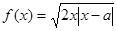 的短距不小于2且长距不大于4 即
的短距不小于2且长距不大于4 即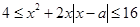 对于
对于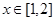

练习册系列答案
相关题目
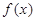 是定义在
是定义在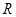 上的奇函数,当
上的奇函数,当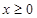 时,
时, .
. ;
;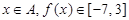 ,求区间
,求区间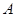 .
.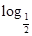 24)的值.
24)的值. ,分别求f1(x)和f2(x);
,分别求f1(x)和f2(x);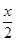 +
+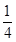 .
.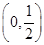 ,使f(x0)=x0.
,使f(x0)=x0.
 .
. 的奇偶性;
的奇偶性; 上为减函数,求
上为减函数,求 的取值范围.
的取值范围. 中,
中, 为奇数,
为奇数, 均为整数,且
均为整数,且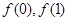 均为奇数.求证:
均为奇数.求证: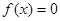 无整数根。
无整数根。 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.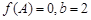 ,求
,求 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围. 是实数,函数
是实数,函数 (
( ).
). 不是奇函数;
不是奇函数; 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的值域(用
的值域(用