题目内容
已知
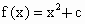 ,且
,且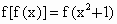 .
.
(1)
设g(x)=f[f(x)],求g(x)的解析式;(2)
设h(x)=g(x)-λf(x),试问:是否存在实数λ,使h(x)在(-∞,-1)内为减函数,且在(-1,0)内是增函数.
答案:略
解析:
提示:
解析:
|
(1)由题意得
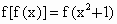 , ,
∴ 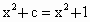 ,即c=1. ,即c=1.
∴ 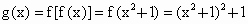 . .
(2) 若满足条件 λ存在,则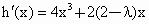 ,∵函数h(x)在(-∞,-1)内为减函数, ,∵函数h(x)在(-∞,-1)内为减函数,
∴当x<-1时, ∴ 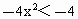 . .
∴2(2 -λ)≥-4,解得λ≤4. ①又函数 h(x)在(-1,0)内是增函数,∴-1<x<0时,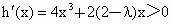 恒成立. 恒成立.
∴ 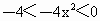 . .
∴2(2 -λ)≤-4,解得λ≥4. ②由 ①②得λ=4时,h(x)在(-∞,-1)内为减函数,且在(-1,0)内是增函数.故满足题设条件的λ存在,且λ=4. |
提示:
|
解析:本题的第 (1)小题可直接由题设求出g(x)解析式,第(2)小题先根据(1)写出h(x),对于探索性问题,一般先对结论肯定存在的假设,然后由此假设出发,根据已知条件进行推理论证. |

练习册系列答案
相关题目
 ,
,



 对x∈(-∞,-1)恒成立.
对x∈(-∞,-1)恒成立.

 ,且
,且 .
.
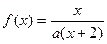 ,方程
,方程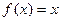 有唯一解,已知
有唯一解,已知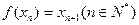 ,且
,且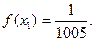
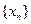 的通项公式;
的通项公式;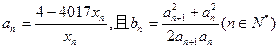 ,求和
,求和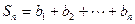 ;
;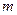 ,使得对任意
,使得对任意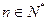 ,有
,有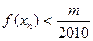 成立,若存在;求出
成立,若存在;求出 ,方程
,方程 有唯一解,已知
有唯一解,已知 ,且
,且
 的通项公式;
的通项公式; ,求和
,求和 ;
; ,使得对任意
,使得对任意 ,有
,有 成立,若存在;求出
成立,若存在;求出