题目内容
(本题满分14分)设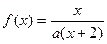 ,方程
,方程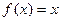 有唯一解,已知
有唯一解,已知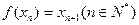 ,且
,且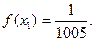
(1)求数列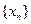 的通项公式;
的通项公式;
(2)若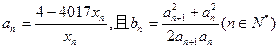 ,求和
,求和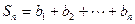 ;
;
(3)问:是否存在最小整数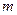 ,使得对任意
,使得对任意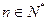 ,有
,有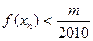 成立,若存在;求出
成立,若存在;求出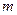 的值;若不存在,说明理由。
的值;若不存在,说明理由。
 ,
, ,存在最小的正整数
,存在最小的正整数
解析解:(1)因为方程
 有唯一解,可求
有唯一解,可求 从而得到
从而得到

 ,
,
又由已知
数列 是首项为
是首项为 ,公差为
,公差为 的等差数列 4分
的等差数列 4分
故 ,
,
所以数列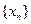 的通项公式为
的通项公式为 6分
6分
(2)将 代入
代入 可求得
可求得


 10分
10分
(3) 恒成立,
恒成立, 只要
只要 即可,
即可,
而 12分
12分
即要 ,故存在最小的正整数
,故存在最小的正整数 14分
14分

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。  .
. ,求函数
,求函数 的极值;
的极值; ,试确定
,试确定 的单调性;
的单调性; ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.