题目内容
设 ,圆
,圆 :
: 与
与 轴正半轴的交点为
轴正半轴的交点为 ,与曲线
,与曲线 的交点为
的交点为 ,直线
,直线 与
与 轴的交点为
轴的交点为 .
.
(1)用 表示
表示 和
和 ;
;
(2)求证: ;
;
(3)设 ,
, ,求证:
,求证: .
.
【答案】
(1) ,
,
(2)根据题意,由于 ,
,
进而得到证明。
(3) 先证:当 时,
时, .然后借助于不等式关系放缩法求和比较大小。
.然后借助于不等式关系放缩法求和比较大小。
【解析】
试题分析:(1)由点 在曲线
在曲线 上可得
上可得 ,
,
又点在圆 上,则
上,则 ,
,
从而直线 的方程为
的方程为 , 由点
, 由点 在直线
在直线 上得:
上得:
 ,将
,将 代入化简得:
代入化简得:  .
.
(2)  ,
,
又 ,
,

(3)先证:当 时,
时, .
.
事实上, 不等式



后一个不等式显然成立,而前一个不等式 .
.
故当 时, 不等式
时, 不等式 成立.
成立.
 ,
,
 (等号仅在n=1时成立)
(等号仅在n=1时成立)
求和得: 

考点:数列的通项公式
点评:解决的关键是根据数列与函数的关系来得到表达式,同时能根据不等式的性质得到放缩法求和,证明不等式,属于中档题。

练习册系列答案
相关题目
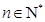 ,圆
,圆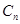 :
: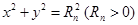 与
与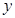 轴正半轴的交点为
轴正半轴的交点为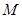 ,与曲线
,与曲线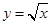 的交点为
的交点为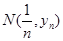 ,直线
,直线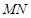 与
与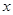 轴的交点为
轴的交点为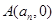 .
.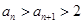 ;
;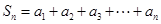 ,
,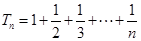 ,求证:
,求证: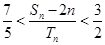 .
.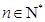 ,圆
,圆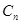 :
: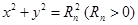 与
与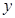 轴正半轴的交点为
轴正半轴的交点为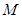 ,与曲线
,与曲线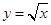 的交点为
的交点为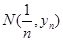 ,直线
,直线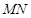 与
与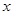 轴的交点为
轴的交点为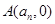 .
.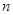 表示
表示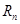 和
和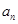 ;
;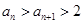 ;
;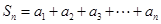 ,
,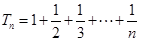 ,求证:
,求证: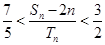 .
.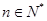 ,圆
,圆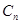 :
: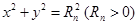 与
与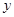 轴正半轴的交点为
轴正半轴的交点为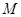 ,与曲线
,与曲线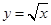 的交点为
的交点为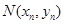 ,直线
,直线 与
与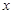 轴的交点为
轴的交点为 .
.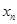 表示
表示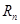 和
和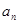 ;
;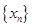 满足:
满足: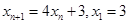 .
. 的值使数列
的值使数列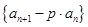 成等比数列;
成等比数列;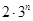 的大小.
的大小.