Question

【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”．已知椭圆，以椭圆的顶点焦点为作相似椭圆．

（Ⅰ）求椭圆的方程；

（Ⅱ）设直线与椭圆交于，两点，且与椭圆仅有一个公共点，试判断的面积是否为定值（为坐标原点）？若是，求出该定值；若不是，请说明理由．

Answer 1

【答案】（Ⅰ）（Ⅱ）的面积为定值6

【解析】

（Ⅰ）椭圆的焦点为椭圆的顶点，故可得椭圆的焦点，离心率与椭圆相同，故可得椭圆；

（Ⅱ）当直线的斜率存在时，设出直线，由直线与椭圆只有一个公共点得出与的等量关系，然后再用与求出的长度、点到直线的距离，从而得出的面积，利用减元思想便可得结果。

解：（Ⅰ）由条件知，椭圆的离心率，且焦点为，，

∴椭圆的方程为；

（Ⅱ）当直线的斜率存在时，设直线．

联立方程组得，

，

因为直线与椭圆仅有一个公共点，

故得，

．

联立方程组，

化简得．

设，，

则 ，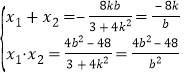

，

原点到直线的距离,

，

当直线的斜率不存在时，

或，则，

原点到直线的距离，

．

综上所述，的面积为定值6