Question

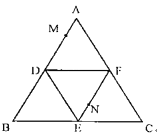
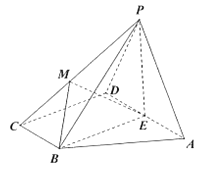
【题目】如图，正三角形的边长为，、、分别为各边的中点，将△沿、、折叠，使、、三点重合，构成三棱锥．

(1)求平面与底面所成二面角的余弦值；

(2)设点、分别在、上， (为变量) ；

①当为何值时，为异面直线与的公垂线段? 请证明你的结论

②设异面直线与所成的角为，异面直线与所成的角为，试求的值．

Answer 1

【答案】（1） （2）①λ=1，证明见解析 ②

【解析】

（1）取DE的中点G，连接AG、FG ，利用正三角形的性质，可以得到∠AGF为平面ADE与底面DEF所成二面角的平面角，最后利用余弦定理求出即可；

（2）①当λ=1，M为AD的中点，N为FF的中点，连结AN、DN，利用等腰三角形的性质可以证明MN⊥AD， MN⊥EF；

②过点M作MH∥DF，交AF于点H，则∠HMN为异面直线 MN与DF所成的角，

通过平行线可以得到比例式子，可以证明∠MNH为异面直线 MN与AE所成的角，求出的表达式，最后利用正棱锥的性质、平行线的性质可以求出的值.

解：（1）如图，取DE的中点G，连接AG、FG

由题意AD=AE，△DEF为正三角形，得AG⊥DE，

∴∠AGF为平面ADE与底面DEF所成二面角的平面角

由题意得AG=FG=．在△AGF中，

∴平面ADE与底面DEF所成二面角的余弦值为

（2）①λ=1时，MN为异面直线AD与EF公垂线段

当λ=1，M为AD的中点，N为FF的中点，连结AN、DN，

则由题意，知AN=DN=，∴MN⊥AD，同理可证MN⊥EF

∴λ=1时，MN为异面直线AD与EF公垂线段．

②过点M作MH∥DF，交AF于点H，则∠HMN为异面直线 MN与DF所成的角 ．

由MH∥DF，得 又，∴

∴HN//AE，∠MNH为异面直线 MN与AE所成的角 ．

∴α+β=∠MNH+∠HMN=π—∠MHN

由题意得，三棱锥A—DEF是正棱锥，则点A在底面DEF上的射影为底面△DEF的中心，记为O．

∵ AE在底面DEF上的射影EO⊥DF， ∴AE⊥DF

又∵HN//AE，MH//DF，∴∠MNH= ，∴