题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,试讨论方程
时,试讨论方程![]() 的解的个数;
的解的个数;
(2)若曲线![]() 和
和![]() 上分别存在点
上分别存在点![]() ,
,![]() ,使得
,使得![]() 是以原点
是以原点![]() 为直角顶点的直角三角形,且斜边
为直角顶点的直角三角形,且斜边![]() 的中点在
的中点在![]() 轴上,求实数
轴上,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)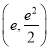
【解析】
(1)求出导函数![]() ,由导函数确定函数的单调性,作出函数的大致图象,通过图象确定方程
,由导函数确定函数的单调性,作出函数的大致图象,通过图象确定方程![]() 解的个数;
解的个数;
(2)设![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,![]() ,题意说明
,题意说明![]() ,代入得
,代入得![]() ,化简后有
,化简后有![]() ,从而
,从而![]() ,只要求得
,只要求得![]() (
(![]() )的值域即得
)的值域即得![]() 的范围.
的范围.
(1)当![]() ,
,![]() ,
,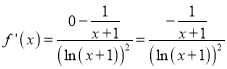 ;
;
又![]() 的定义域为
的定义域为![]() ;
;
当![]() 时,
时,![]() 恒成立.
恒成立.
所以,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 也单调递减,图象如图所示.
也单调递减,图象如图所示.
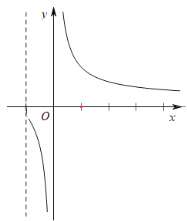
因此,当![]() 即
即![]() 时,方程无解;
时,方程无解;
当![]() 即
即![]() 时,方程有唯一解.
时,方程有唯一解.
(2)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,∴
,∴![]() .
.
![]() ,
,![]() ,
,
由题意,![]() ,即
,即
![]() ,
,
∴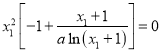 ,
,
∵![]() ,
,
∴![]() ,
,
则![]() .
.
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
即函数![]() 在
在![]() 上为增函数,
上为增函数,
则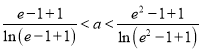 ,
,
即![]() .
.
∴实数![]() 的取值范围是
的取值范围是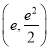 .
.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目