题目内容
20.已知函数f(x)的定义域为R,当x>0时,f(x)=log2x;当-1≤x≤1时,f(x)+f(-x)=0;当$x<-\frac{1}{2}$时,$f(x-\frac{1}{2})-f(x+\frac{1}{2})=0$.则$f(-32)+f(-\frac{1}{32})$的值为5.分析 由已知分析出当-1≤x≤1时的奇偶性和当$x<-\frac{1}{2}$时的周期性,进而可得答案.
解答 解:∵当x>0时,f(x)=log2x;
∴f(1)=0,f($\frac{1}{32}$)=-5,
∵当-1≤x≤1时,f(x)+f(-x)=0;
∴f(-$\frac{1}{32}$)+f($\frac{1}{32}$)=0,即f(-$\frac{1}{32}$)=5,
同理:f(-1)=0
又∵当$x<-\frac{1}{2}$时,$f(x-\frac{1}{2})-f(x+\frac{1}{2})=0$.
故f(-32)=f(-31)=f(-30)=…=f(-1)=0,
故$f(-32)+f(-\frac{1}{32})$=5,
故答案为:5.
点评 本题考查的知识点是抽象函数的应用,函数的奇偶性,函数的周期性,函数的求值,难度中档.

练习册系列答案
相关题目
19.在实数集R中定义一种运算“⊙”,具有性质:①对任意a、b∈R,a⊙b=b⊙a;②a⊙0=a;③对任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)-2c,则函数f(x)=x⊙$\frac{1}{x}({x>0})$的最小值是( )
| A. | 2 | B. | 3 | C. | $3\sqrt{2}$ | D. | $2\sqrt{2}$ |
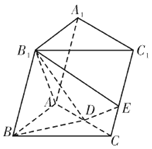 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.