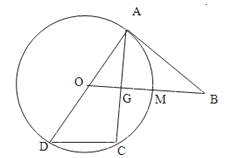
题目内容
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
【答案】(1) ![]() ,
, ![]() ;(2)
;(2)![]()
【解析】
(1)根据条件列方程组解得a,b,根据抛物线焦点坐标所在位置可设抛物线方程形式,再根据焦点坐标求抛物线标准方程,(2)利用斜率设直线![]() 、OB方程,分别与抛物线、椭圆方程联立方程组解得A,B横坐标,再根据A,B横坐标和为0解斜率得A,B坐标,最后根据两点式求直线AB 方程.
、OB方程,分别与抛物线、椭圆方程联立方程组解得A,B横坐标,再根据A,B横坐标和为0解斜率得A,B坐标,最后根据两点式求直线AB 方程.
(1) 由![]() 得
得![]() ,又有
,又有![]() ,代入
,代入![]() ,解得
,解得![]()
所以椭圆方程为![]()
由抛物线的焦点为![]() 得,抛物线焦点在
得,抛物线焦点在![]() 轴,且
轴,且![]() ,
,
抛物线的方程为:![]()
(2)由题意点![]() 位于第一象限,可知直线
位于第一象限,可知直线![]() 的斜率一定存在且大于
的斜率一定存在且大于![]()
设直线![]() 方程为:
方程为:![]() ,
,![]()
联立方程![]() 得:
得:![]() ,可知点
,可知点![]() 的横坐标
的横坐标![]() ,即
,即![]()
因为![]() ,可设直线
,可设直线![]() 方程为:
方程为:![]()
连立方程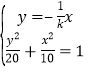 得:
得:![]() ,从而得
,从而得![]()
若线段![]() 的中点在
的中点在![]() 轴上,可知
轴上,可知![]() ,即
,即![]()
有![]() ,且
,且![]() ,解得
,解得![]()
从而得![]() ,
,![]()
直线![]() 的方程:
的方程:![]()

练习册系列答案
相关题目