题目内容
已知圆C:(x-a)2+(y-2)2=4(a>0)及直线l:x-y+3=0,当直线l被圆C截得的弦长为2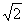 时,
时,
求:(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程。
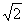 时,
时,求:(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程。
解:(Ⅰ)依题意可得圆心C(a,2),半径r=2,
则圆心到直线l:x-y+3=0的距离 ,
,
由勾股定理可知, ,
,
代入化简得|a+1|=2,解得a=1或a=-3,
又a>0,所以a=1。
(Ⅱ)由(1)知圆 ,
,
又(3,5)在圆外,
∴①当切线方程的斜率存在时,设方程为y-5=k(x-3),
由圆心到切线的距离d=r=2,可解得 ,
,
∴切线方程为5x-12y+45=0;
②当过(3,5)斜率不存在,直线方程为x=3与圆相切;
由①②可知切线方程为5x-12y+45=0或x=3。
则圆心到直线l:x-y+3=0的距离
 ,
,由勾股定理可知,
 ,
,代入化简得|a+1|=2,解得a=1或a=-3,
又a>0,所以a=1。
(Ⅱ)由(1)知圆
 ,
,又(3,5)在圆外,
∴①当切线方程的斜率存在时,设方程为y-5=k(x-3),
由圆心到切线的距离d=r=2,可解得
 ,
,∴切线方程为5x-12y+45=0;
②当过(3,5)斜率不存在,直线方程为x=3与圆相切;
由①②可知切线方程为5x-12y+45=0或x=3。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 距离的最小值等于 .
距离的最小值等于 .