题目内容
顶点在原点,焦点是(0,5)的抛物线方程是( )A.x2=20y
B.y2=20
C.y2=
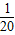
D.x2=
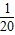 y
y
【答案】分析:利用抛物线的性质即可求得答案.
解答:解:∵抛物线的顶点在原点,焦点是(0,5),焦点在y轴的正半轴,
∴设抛物线的方程为x2=2py,(p>0),
则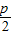 =5,
=5,
∴p=10.
∴抛物线的方程为x2=2×10y=20y.
故选A.
点评:本题考查抛物线的标准方程,由焦点位置确定方程类型及p的值是关键,属于基础题.
解答:解:∵抛物线的顶点在原点,焦点是(0,5),焦点在y轴的正半轴,
∴设抛物线的方程为x2=2py,(p>0),
则
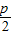 =5,
=5,∴p=10.
∴抛物线的方程为x2=2×10y=20y.
故选A.
点评:本题考查抛物线的标准方程,由焦点位置确定方程类型及p的值是关键,属于基础题.

练习册系列答案
相关题目
已知圆F的方程是x2+y2-2y=0,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为α的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若|AB|,|BC|,|CD|成等差数列,则α的值为( )
A、±arctan
| ||||||||
B、
| ||||||||
C、arctan
| ||||||||
D、arctan
|