题目内容
已知函数f(x)=
(1)求函数的定义域和值域;
(2)证明:f(x)是单调函数.
| 2x-2-x |
| 2x+2-x |
(1)求函数的定义域和值域;
(2)证明:f(x)是单调函数.
考点:函数单调性的判断与证明,函数的定义域及其求法,函数的值域
专题:函数的性质及应用
分析:(1)化简函数f(x)的解析式,求出函数的定义域与值域为;
(2)用单调性的定义即可证明f(x)是定义域上的单调函数.
(2)用单调性的定义即可证明f(x)是定义域上的单调函数.
解答:
解:(1)∵函数f(x)=
=
=1-
,
且4x+1>1,∴f(x)的定义域为R;
又0<
<1,
∴-2<-
<0,
∴-1<1-
<1,
∴f(x)的值域为(-1,1);
(2)证明:任取x1、x2∈R,且x1<x2,
∴f(x1)-f(x2)=(1-
)-(1-
)
=
-
=
;
∵x1<x2,
∴2(4x1-4x2)<0,(4x1+1)(4x2+1)>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2);
∴f(x)是定义域R上的单调增函数.
| 2x-2-x |
| 2x+2-x |
| 22x-1 |
| 22x+1 |
| 2 |
| 4x+1 |
且4x+1>1,∴f(x)的定义域为R;
又0<
| 1 |
| 4x+1 |
∴-2<-
| 2 |
| 4x+1 |
∴-1<1-
| 2 |
| 4x+1 |
∴f(x)的值域为(-1,1);
(2)证明:任取x1、x2∈R,且x1<x2,
∴f(x1)-f(x2)=(1-
| 2 |
| 4x1+1 |
| 2 |
| 4x2+1 |
=
| 2 |
| 4x2+1 |
| 2 |
| 4x1+1 |
=
| 2(4x1-4x2) |
| (4x1+1)(4x2+1) |
∵x1<x2,
∴2(4x1-4x2)<0,(4x1+1)(4x2+1)>0,
∴f(x1)-f(x2)<0,
即f(x1)<f(x2);
∴f(x)是定义域R上的单调增函数.
点评:本题考查了根据函数的解析式求定义域和值域的问题,也考查了根据单调性的定义证明函数的单调性问题,是基础题目.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
若函数f(x)满足:?x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤|x1-x2|成立,则称f(x)∈Ψ.对于函数g(x)=x3-x,h(x)=
,有( )
|
| A、g(x)∈Ψ且h(x)∈Ψ |
| B、g(x)∈Ψ且h(x)∉Ψ |
| C、g(x)∉Ψ且h(x)∈Ψ |
| D、g(x)∉Ψ且h(x)∉Ψ |
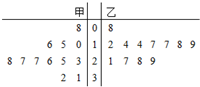 如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为
如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=
,则
的值是( )
| x |
| lim |
| △x→0 |
| f(x-△x)-f(x) |
| △x |
A、-
| ||||
B、
| ||||
C、-
|