题目内容
函数y= x2-lnx的单调递减区间为( )
x2-lnx的单调递减区间为( )A.(-1,1]
B.(0,1]
C.[1,+∞)
D.(0,+∞)
【答案】分析:由y= x2-lnx得y′=
x2-lnx得y′=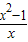 ,由y′≤0即可求得函数y=
,由y′≤0即可求得函数y= x2-lnx的单调递减区间.
x2-lnx的单调递减区间.
解答:解:∵y= x2-lnx的定义域为(0,+∞),
x2-lnx的定义域为(0,+∞),
y′=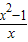 ,
,
∴由y′≤0得:0<x≤1,
∴函数y= x2-lnx的单调递减区间为(0,1].
x2-lnx的单调递减区间为(0,1].
故选B.
点评:本题考查利用导数研究函数的单调性,注重标根法的考查与应用,属于基础题.
 x2-lnx得y′=
x2-lnx得y′=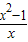 ,由y′≤0即可求得函数y=
,由y′≤0即可求得函数y= x2-lnx的单调递减区间.
x2-lnx的单调递减区间.解答:解:∵y=
 x2-lnx的定义域为(0,+∞),
x2-lnx的定义域为(0,+∞),y′=
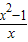 ,
,∴由y′≤0得:0<x≤1,
∴函数y=
 x2-lnx的单调递减区间为(0,1].
x2-lnx的单调递减区间为(0,1].故选B.
点评:本题考查利用导数研究函数的单调性,注重标根法的考查与应用,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
求函数y=x2-lnx图象上一点到直线y=x-2的最小距离( )
A、
| ||||
| B、2 | ||||
| C、1 | ||||
D、
|