题目内容
5.若f(x)是定义R在上的奇函数,当x<0时f(x)=cos3x+sin2x,则当x>0时,f(x)=-cos3x+sin2x.分析 根据x<0时,有f(x)=cos3x+sin2x,可得x>0时,-x<0满足函数的解析式,进而根据函数f(x)是奇函数,f(x)=-f(-x)得到当x>0时,f(x)的表达式.
解答 解:当x>0时,-x<0时,
∵当x<0时,有f(x)=cos3x+sin2x,
∴当x>0时,-x<0时,f(-x)=cos(-3x)+sin(-2x)=cos3x-sin2x,
又∵函数f(x)是奇函数,
∴当x>0时,f(x)=-f(-x)=-cos3x+sin2x
故答案为:-cos3x+sin2x.
点评 本题考查的知识点是函数解析式的求解及常用方法,熟练掌握奇函数的性质是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | 60-12π | B. | 60-6π | C. | 72-12π | D. | 72-6π |
15.张君四年前买了50000元的某种基金,收益情况是前两年每年递减20%,后两年每年递增20%,则现在的价值与原来价值比较,变化的情况是( )
| A. | 减少7.84% | B. | 增加7.84% | C. | 减少9.5% | D. | 增加 |
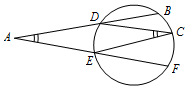 所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.
所谓弧的度数指的是弧所对的圆心角的度数,如图,$\widehat{BC}$,$\widehat{CF}$的度数分别为62°,68°,则∠BAF+∠DCE=65°.