题目内容
 ,若A∩B≠φ,则a的取值范围是
,若A∩B≠φ,则a的取值范围是
- A.
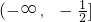
- B.
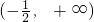
- C.

- D.(-∞,-2]
A
分析:先化简集合A,B,欲使A∩B≠φ,即要使A,B有公同元素,结合集合的数轴表示,即可得出a的取值范围.
解答: 解:∵A={-2,-
解:∵A={-2,- },
},
B=[a,+∞);
结合数轴表示,得到:
若A∩B≠φ,则a的取值范围是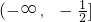 .
.
故选A.
点评:本题属于以函数的值域为平台,考查求集合的交集的基础题,也是高考常会考的题型.
分析:先化简集合A,B,欲使A∩B≠φ,即要使A,B有公同元素,结合集合的数轴表示,即可得出a的取值范围.
解答:
 解:∵A={-2,-
解:∵A={-2,- },
},B=[a,+∞);
结合数轴表示,得到:
若A∩B≠φ,则a的取值范围是
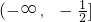 .
.故选A.
点评:本题属于以函数的值域为平台,考查求集合的交集的基础题,也是高考常会考的题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题中正确的是( )
A、若
| ||||||||||||
B、若
| ||||||||||||
C、若
| ||||||||||||
D、若
|
对于向量
、
,下列命题正确的是( )
| a |
| b |
A、若
| ||||||||||||||||
B、(
| ||||||||||||||||
C、若|
| ||||||||||||||||
D、若
|