题目内容
已知
(1)求函数 的最小值;
的最小值;
(2)对一切 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有 成立.
成立.
(1)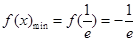 ;(2)
;(2) (3)见解析
(3)见解析
解析试题分析:(1)先求定义域,再利用导数与单调性的关系求单调区间;(2)通过导数解决不等式恒成立的问题;(3)先转化不等式,在给定的区间内比较大小.
(1)由已知知函数 的定义域为
的定义域为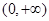 ,
,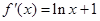 , 1分
, 1分
当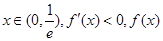 单调递减, 2分
单调递减, 2分
当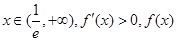 单调递增. 3分
单调递增. 3分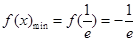 . 4分
. 4分
(2)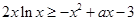 ,则
,则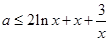 , 5分
, 5分
设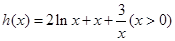 ,则
,则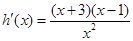 , 6分
, 6分
①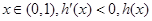 单调递减;
单调递减;
②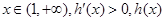 单调递增;
单调递增;
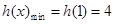 ,对一切
,对一切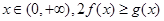 恒成立,
恒成立,
 . 8分
. 8分
(3)原不等式等价于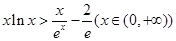 , 9分
, 9分
由(1)可知 的最小值是
的最小值是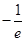 ,当且仅当
,当且仅当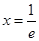 时取到最小值. 10分
时取到最小值. 10分
设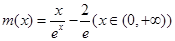 ,则
,则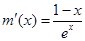 ,
,
易知 ,当且仅当
,当且仅当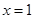 时取到最小值.[来源:学&科&
时取到最小值.[来源:学&科&
从而对一切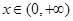 ,都有
,都有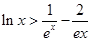 成立. 12分
成立. 12分
考点:利用导数求单调区间;函数单调性;不等式恒成立。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值; +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称. ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
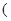 常数
常数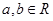 )满足
)满足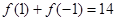 .
. 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;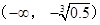 上单调递减,求
上单调递减,求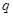 且存在递增的正整数数列
且存在递增的正整数数列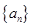 ,使得
,使得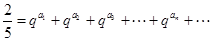 成立.
成立. 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.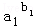
 …
…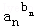 ≤1;
≤1; ≤
≤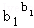
 …
…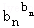 ≤b12+b22+…+bn2.
≤b12+b22+…+bn2. 其中0
其中0
 上恒成立?
上恒成立? 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
 ,当
,当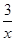 )元.
)元.