题目内容
已知f(x)=ex-t(x+1).
(Ⅰ)若f(x)≥0对一切正实数x恒成立,求t的取值范围;
(Ⅱ)设 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
(Ⅲ)求证: (n∈N*).
(n∈N*).
1) (x>0)恒成立。
(x>0)恒成立。
设 (x≥0),则
(x≥0),则
∴ 在
在 时单调递增,
时单调递增, (x=1时取等号),
(x=1时取等号),
∴t≤1 ………4分
(2)设x1、x2是任意的两实数,且x1<x2
 ,故
,故
设 ,则F(x)在R上单调递增, ………7分
,则F(x)在R上单调递增, ………7分
即 恒成立。
恒成立。
即对任意的t≤-1,x∈R, 恒成立。
恒成立。
而
故m<3 ………9分
(3)由(1)知,
取 ,则
,则


∴ (n∈N*) ………14分
(n∈N*) ………14分

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案总体由编号分别为01,02,…,19,20的20个个体组成。利用下面的随机数表选取5个个体,选取
方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的
第5个个体的编号为
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4935 8200 3623 4869 6938 7481 |
A.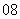 B.
B.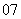 C.
C.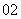 D.
D.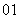
 =-sin
=-sin ,则角
,则角 的最大值为( )
的最大值为( ) D.2-
D.2- 。设
。设 ,
, ,且顶点B、C分别在两条平行直线上运动,则
,且顶点B、C分别在两条平行直线上运动,则 的最大值为_______.
的最大值为_______.
 是纯虚数,则
是纯虚数,则 ( )
( ) B.
B. C.
C.
 与双曲线
与双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若 为双曲线的一条渐近线,则
为双曲线的一条渐近线,则 B.
B.  C.
C. D.
D. 
 的部分图像,其中A,B两点之间的距离为5,那么
的部分图像,其中A,B两点之间的距离为5,那么 ( )
( )
 D.1
D.1