题目内容
椭圆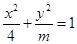 的焦距为2,则
的焦距为2,则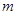 的值为( )
的值为( )
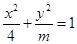 的焦距为2,则
的焦距为2,则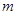 的值为( )
的值为( )| A.3 | B.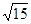 | C.3或5 | D.3或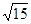 |
C
试题分析:椭圆
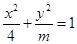 焦点在x轴时:
焦点在x轴时:
 ;当焦点在y轴时:
;当焦点在y轴时:
 ,综上
,综上 或
或
点评:椭圆焦点位置的判定是看标准方程中
 对应的分母,哪一个较大,则焦点就在哪一个轴上,,本题中焦点位置不确定,因此需分情况讨论,椭圆中
对应的分母,哪一个较大,则焦点就在哪一个轴上,,本题中焦点位置不确定,因此需分情况讨论,椭圆中

练习册系列答案
相关题目
题目内容
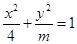 的焦距为2,则
的焦距为2,则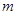 的值为( )
的值为( )| A.3 | B.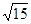 | C.3或5 | D.3或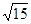 |
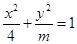 焦点在x轴时:
焦点在x轴时:
 ;当焦点在y轴时:
;当焦点在y轴时:
 ,综上
,综上 或
或
 对应的分母,哪一个较大,则焦点就在哪一个轴上,,本题中焦点位置不确定,因此需分情况讨论,椭圆中
对应的分母,哪一个较大,则焦点就在哪一个轴上,,本题中焦点位置不确定,因此需分情况讨论,椭圆中
