题目内容
已知二次函数f(x)=ax2+bx+c(a≠0)且满足f(-1)=0,对任意实数x,恒有f(x)-x≥0,并且当x∈(0,2)时,有f(x)≤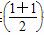 2.
2.
(1)求f(1)的值;
(2)证明a>0,c>0;
(3)当x∈[-1,1]时,函数g(x)=f(x)-mx(x∈R)是单调函数,求证:m≤0或m≥1.
(1)对x∈R,f(x)-x≥0恒成立,
当x=1时,f(1)≥1,
又∵1∈(0,2),由已知得f(1)≤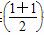 2=1,
2=1,
∴1≤f(1)≤1,∴f(1)=1.
(2)证明:∵f(1)=1,f(-1)=0,∴a+b+c=1,
a-b+c=0,∴b=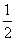 .∴a+c=
.∴a+c=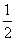 .
.
∵f(x)-x≥0对x∈R恒成立,
∴ax2-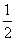 x+c≥0对x∈R恒成立,
x+c≥0对x∈R恒成立,
∴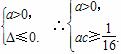 ∴c>0,故a>0,c>0.
∴c>0,故a>0,c>0.
(3)证明:∵a+c=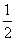 ,ac≥
,ac≥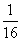 ,由a>0,c>0及a+c≥2
,由a>0,c>0及a+c≥2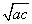 ,得ac≤
,得ac≤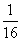 ,∴ac=
,∴ac=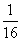 ,当且仅当a=c=
,当且仅当a=c=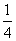 时,取“=”.
时,取“=”.
∴f(x)=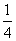 x2+
x2+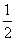 x+
x+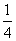 .
.
∴g(x)=f(x)-mx=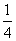 x2+
x2+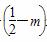 x+
x+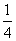 =
=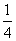 [x2+(2-4m)x+1].
[x2+(2-4m)x+1].
∵g(x)在[-1,1]上是单调函数,
∴2m-1≤-1或2m-1≥1,∴m≤0或m≥1.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 x+
x+
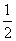 B.
B.
 D.
D.
 B.
B.