题目内容
如图，所有棱长都为2的正三棱柱BCD-B′C′D′，四边形ABCD是菱形，其中E为BD的中点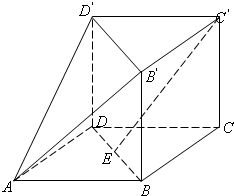
（Ⅰ）求证：平面BC′D∥面AB′D′；
（Ⅱ）求面AB′D′与面ABD所成锐二面角的余弦值．
（Ⅰ）求证：平面BC′D∥面AB′D′；
（Ⅱ）求面AB′D′与面ABD所成锐二面角的余弦值．
考点：二面角的平面角及求法,平面与平面平行的判定
专题：空间位置关系与距离,空间角
分析：（Ⅰ）取B′D′的中点为F，连AF，C′F，由已知得AFC′E为平行四边形，由此能证明平面BC′D∥面AB′D′．
（Ⅱ）连结EF，由已知得面AB′D′与面ABD所成锐二面角为∠EAF，由此能求出面AB′D′与面ABD所成锐二面角的余弦值．
（Ⅱ）连结EF，由已知得面AB′D′与面ABD所成锐二面角为∠EAF，由此能求出面AB′D′与面ABD所成锐二面角的余弦值．
解答：
（Ⅰ）证明：如图取B′D′的中点为F，连AF，C′F，
∵正三棱柱BCD-B′C′D′，四边形ABCD是菱形，
∴B′D′∥BD，C′F
AE，∴AFC′E为平行四边形．
∴AF∥C′E，又BD∩C′E=E，
∴平面BC′D∥面AB′D′．
（Ⅱ）解：连结EF，由已知得EF⊥平面ABD，
∴面AB′D′与面ABD所成锐二面角为∠EAF，
∵所有棱长都为2的正三棱柱BCD-B′C′D′，
四边形ABCD是菱形，
∴EF=2，AE=
=
，AF=
=
，
∴cos∠EAF=
=
=
，
∴面AB′D′与面ABD所成锐二面角的余弦值为
．
∵正三棱柱BCD-B′C′D′，四边形ABCD是菱形，
∴B′D′∥BD，C′F
| ∥ |
. |
∴AF∥C′E，又BD∩C′E=E，
∴平面BC′D∥面AB′D′．
（Ⅱ）解：连结EF，由已知得EF⊥平面ABD，
∴面AB′D′与面ABD所成锐二面角为∠EAF，
∵所有棱长都为2的正三棱柱BCD-B′C′D′，
四边形ABCD是菱形，
∴EF=2，AE=
| 4-1 |
| 3 |
| 4+3 |
| 7 |
∴cos∠EAF=
| AE |
| AF |
| ||
|
| ||
| 7 |
∴面AB′D′与面ABD所成锐二面角的余弦值为
| ||
| 7 |
点评：本题主要考查直线与平面之间的平行、垂直等位置关系，线线角、线面角、二面角的概念、求法等知识，以及空间想象能力和逻辑推理能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
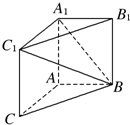如图，在三棱柱ABCA1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．设点P在曲线y=x2上，点Q在直线y=2x-2上，则PQ的最小值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
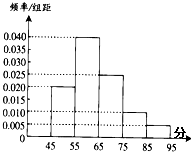为了调查某班学生做数学题的基本能力，随机抽查了部分学生某次做一份满分为100分的数学试题，他们所得分数的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95），由此得到频率分布直方图如图，则这些学生的平均分为
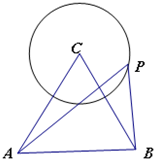如图，△ABC是边长为2ρ=
（cosθ-sinθ）（ρ＞0）的圆心极坐标为（ ）
| 2 |
A、（-1，
| ||||
B、（1，
| ||||
C、（
| ||||
D、（1，
|