题目内容
4．若$\frac{sinαcosα}{cos2α+1}=1，tan（{α-β}）=3$，则tanβ=（ ）| A． | -1 | B． | $\frac{1}{7}$ | C． | $-\frac{1}{7}$ | D． | 1 |
分析 由已知利用二倍角的余弦函数公式，同角三角函数基本关系式可求tanα=2，进而利用两角差的正切函数公式即可化简已知等式得解．
解答 解：∵$\frac{sinαcosα}{cos2α+1}=1$，可得：$\frac{sinαcosα}{2co{s}^{2}α}$=1，可得：$\frac{tanα}{2}=1$，即：tanα=2，
∴由tan（α-β）=3=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{2-tanβ}{1+2tanβ}$，
解得：tan$β=-\frac{1}{7}$，
故选：C．
点评 本题主要考查了二倍角的余弦函数公式，同角三角函数基本关系式，两角差的正切函数公式在三角函数化简求值中的应用，考查了转化思想，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
14．已知奇函数f（x）满足f（x-2）=f（x），当0＜x＜l时，f（x）=2x，则f（log29）的值为（ ）
| A． | 9 | B． | -$\frac{1}{9}$ | C． | -$\frac{16}{9}$ | D． | $\frac{16}{9}$ |
12．已知非零向量$\overrightarrow a，\overrightarrow b$满足$（{\overrightarrow b-2\overrightarrow a}）⊥\overrightarrow b$，且$\overrightarrow a⊥（\overrightarrow a-2\overrightarrow b）$，则$\overrightarrow a$与$\overrightarrow b$的夹角是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{2}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
9．若将函数y=2cos2x的图象向右平移$\frac{π}{12}$个单位长度，则平移后函数的一个零点是（ ）
| A． | （$\frac{5}{6}$π，0） | B． | （$\frac{7π}{6}$，0） | C． | （-$\frac{π}{3}$，0） | D． | （$\frac{π}{6}$，0） |
16．直线x+y-1=0的倾斜角等于（ ）
| A． | 45° | B． | 60° | C． | 120° | D． | 135° |
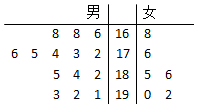M公司从某大学招收毕业生，经过综合测试，录用了14名男生和6名女生，这20名毕业生的测试成绩如茎叶图所示（单位：分），公司规定：成绩在180分以上者到“甲部门”工作；180分以下者到“乙部门”工作．