题目内容
15.如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.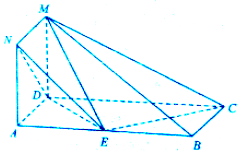
(1)若点E是AB的中点,求证:BM∥平面NDE;
(2)若二面角D-CE-M的大小为$\frac{π}{6}$,求出AE的长.
分析 (1)连结AM,设AM∩ND=F,连结EF,推导出EF∥BM,由此能证明BM∥平面NDE.
(2)以D为坐标原点,DA,DC,DM为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角D-CE-M的大小为$\frac{π}{6}$时,AE的长.
解答 证明:(1)连结AM,设AM∩ND=F,连结EF,
∵四边形ADMN为正方形,∴F是AM的中点,
又∵E是AB中点,∴EF∥BM,
又∵EF?平面NDE,BM?平面NDE,
∴BM∥平面NDE.
解:(2)∵MD⊥AD,平面ADMN⊥平面ABCD,交线为AD,MD?平面ADMN,
∴MD⊥平面ABCD,又∵AD⊥DC,
∴以D为坐标原点,DA,DC,DM为x,y,z轴,建立空间直角坐标系,
则D(0,0,0),C(0,6,0),M(0,0,3),
设AE=a,(0≤a≤6),则E(3,a,0),$\overrightarrow{EC}$=(-3,6-a,0),$\overrightarrow{MC}$=(0,6,-3),
设平面CEM的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{-3x+(6-a)y=0}\\{6y-3z=0}\end{array}\right.$,令y=1,得x=$\frac{6-a}{3}$,z=2,
∴$\overrightarrow{n}$=($\frac{6-a}{3}$,1,2),
又∵平面DCE的一个法向量为$\overrightarrow{m}$=(0,0,1),且二面角的大小为$\frac{π}{6}$,
∴cos$\frac{π}{6}$=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{2}{1×\sqrt{(\frac{6-a}{3})^{2}+1+4}}$,解得a=6-$\sqrt{3}$,(0≤a≤6),
由二面角D-CE-M的大小为$\frac{π}{6}$,
可得AE=6-$\sqrt{3}$.
点评 本题考查线面平行的证明,考查二面角的求法及应用,是中档题,解题时要认真审题,注意空间思维能力培养和向量法的合理运用.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | $\frac{x^2}{25}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}-\frac{y^2}{16}=1({x≠±5})$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1({x≠±5})$ |
| A. | 向左平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向右平移$\frac{π}{12}$个单位长度 |
| A. | -1 | B. | $\frac{1}{7}$ | C. | $-\frac{1}{7}$ | D. | 1 |
 在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.
在长方体ABCD-A1B1C1D1中,AB=BC=$\sqrt{2}$AA1,Q是棱CC1上的动点,则当BQ+D1Q的长度取得最小值时,直线B1Q和直线BD所成的角的正切值是$\frac{\sqrt{5}}{2}$.