题目内容
9.如图,在△ABC中,点D在边AB上,∠BCD=60°,AC=$\sqrt{7}$,CD=2,BD=2AD,则AD=$\sqrt{3}$或1.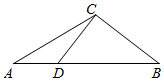
分析 设AD=x,则BD=2x,AB=3x,先在△ACD中利用余弦定理求出cosA,再在△ABC中使用余弦定理计算BC2,最后在△BCD中使用余弦定理列方程解出x.
解答 解:设AD=x,则BD=2x,AB=3x.
在△ACD中,由余弦定理得cosA=$\frac{A{C}^{2}+A{D}^{2}-C{D}^{2}}{2AC•AD}$=$\frac{{x}^{2}+3}{2\sqrt{7}x}$.
在△ABC中,由余弦定理得BC2=AC2+AB2=2AC•AB•cosA=7+9x2-2$•\sqrt{7}•3x•\frac{{x}^{2}+3}{2\sqrt{7}x}$=6x2-2.
在△BCD中,由余弦定理得cos∠BCD=$\frac{B{C}^{2}+C{D}^{2}-B{D}^{2}}{2BC•CD}$,即$\frac{1}{2}$=$\frac{2{x}^{2}+2}{4\sqrt{6{x}^{2}-2}}$,解得x=1或x=$\sqrt{3}$.
故答案为:1或$\sqrt{3}$.
点评 本题考查了余弦定理的应用,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.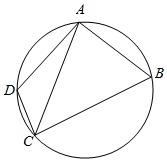 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
 如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )
如图,圆内接四边形ABCD中,AB=2,BC=4,∠ABC=60° 顶点D在劣弧$\widehat{AC}$上运动,则三角形ACD面积的最大值等于( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
20.已知全集U=R,集合A={x|(x+2)(x-2)≤0},则集合∁RA=( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2]∪[2,+∞) |
17.已知等比数列{an}单调递减,满足a1a5=9,a2+a4=10,则数列{an}的公比q=( )
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 3 |
1.“x>2”是“x2-2x>0”成立的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
18.已知z是纯虚数,i为虚数单位,$\frac{z+2}{1-i}$在复平面内所对应的点在实轴上,那么z等于( )
| A. | 2i | B. | i | C. | -i | D. | -2i |
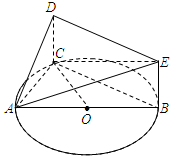 如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.
如图,AB是△ABC外接圆O的直径,四边形DCBE为矩形,且DC⊥平面ABC,AB=4,BE=1.