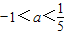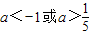题目内容
设f(x)=3ax-2a+1,若存在x0∈(-1,1),使f(x0)=0,则实数a的取值范围是______.
∵f(x)=3ax-2a+1,
当a≠0时,函数有且只有一个零点
若存在x0∈(-1,1),使f(x0)=0,
则f(-1)•f(1)<0
即(-3a-2a+1)•(3a-2a+1)<0
即(-5a+1)•(a+1)<0
解得a<-1或a>
故实数a的取值范围是a<-1或a>
故答案为:a<-1或a>
当a≠0时,函数有且只有一个零点
若存在x0∈(-1,1),使f(x0)=0,
则f(-1)•f(1)<0
即(-3a-2a+1)•(3a-2a+1)<0
即(-5a+1)•(a+1)<0
解得a<-1或a>
| 1 |
| 5 |
故实数a的取值范围是a<-1或a>
| 1 |
| 5 |
故答案为:a<-1或a>
| 1 |
| 5 |

练习册系列答案
相关题目
设f(x)=3ax-2a+1,若存在x0∈(-1,1),使f(x0)=0,则实数a的取值范围是( )
A、-1<a<
| ||
| B、a<-1 | ||
C、a<-1或a>
| ||
D、a>
|