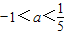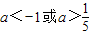Question

设f（x）=3ax-2a+1，若存在x₀∈（-1，1），使f（x₀）=0，则实数a的取值范围是

 

．

Answer 1

分析：由已知中函数f（x）=3ax-2a+1，我们可得当a≠0时，函数为一次函数，有且只有一个零点，若存在x₀∈（-1，1），使f（x₀）=0，根据零点存在定理，我们易得f（-1）•f（1）＜0，代入可以得到一个关于a的不等式，解不等式即可得到答案．

解答：解：∵f（x）=3ax-2a+1，
当a≠0时，函数有且只有一个零点
若存在x₀∈（-1，1），使f（x₀）=0，
则f（-1）•f（1）＜0
即（-3a-2a+1）•（3a-2a+1）＜0
即（-5a+1）•（a+1）＜0
解得a＜-1或a＞

1

5

故实数a的取值范围是a＜-1或a＞

1

5

故答案为：a＜-1或a＞

1

5

点评：本题考查的知识点是函数零点的判定定理，其中根据一次函数只有一个零点及零点判定定理构造关于a的不等式，是解答本题的关键．