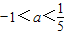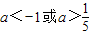题目内容
设f（x）=3ax-2a+1，a为常数．若存在x0∈（0，1），使得f（x0）=0，则实数a的取值范围是分析：因为存在x0∈（0，1），使得f（x0）=0，所以函数f（x）在（0，1）上有零点，因此f（0）×f（1）＜0．
解答：解：因为存在x0∈（0，1），使得f（x0）=0，
所以函数f（x）在（0，1）上有零点，
因此f（0）×f（1）＜0，即：（1-2a）（a+1）＜0
解得：a＜-1或a＞
，故答案为：(-∞，-1)∪(
，+∞)．
所以函数f（x）在（0，1）上有零点，
因此f（0）×f（1）＜0，即：（1-2a）（a+1）＜0
解得：a＜-1或a＞
| 1 |
| 2 |
| 1 |
| 2 |
点评：考查函数的零点与对应方程根的关系，以及对函数零点存在性定理的理解掌握程度．
练习册系列答案
相关题目
设f（x）=3ax-2a+1，若存在x0∈（-1，1），使f（x0）=0，则实数a的取值范围是（ ）
A、-1＜a＜
| ||
| B、a＜-1 | ||
C、a＜-1或a＞
| ||
D、a＞
|
