题目内容
如图,△CDE中∠CDE=90°,平面CDE外一条线段AB满足AB∥DE,AB=![]() DE,AB⊥AC,F是CD的中点.
DE,AB⊥AC,F是CD的中点.
(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)若AC=AD,证明:AF⊥平面CDE.

考点:
直线与平面平行的判定;直线与平面垂直的判定;直线与平面垂直的性质.
专题:
空间位置关系与距离.
分析:
(I)在平面BCE内作AF的平行线,通过线线平行证明线面平行;
(II)根据线面垂直的性质证线线垂直,再由线线垂直⇒线面垂直.
解答:
解:(I)取CE的中点O,连接BO、OF.
∵O、F分别是CD与CE的中点,∴OF∥DE,OF=![]() DE,
DE,
又AB∥DE,AB=![]() DE,∴四边形ABOF为平行四边形,∴AF∥BO
DE,∴四边形ABOF为平行四边形,∴AF∥BO
AF⊄平面BCE,BO⊂平面BCE,
∴AF∥平面BCE.
(II)∵AB⊥AC,AB∥DE,∴DE⊥AC,
又DE⊥CD,CD∩AC=C,∴DE⊥平面ACD
∵AF⊂平面ACD,∴AF⊥DE;
∵F是CD的中点,AC=AD,∴AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE.

点评:
本题考查线面平行的判定及线面垂直的判定.线面平行的证明方法:1、线线平行⇒线面平行;2、面面平行⇒线面平行.线面垂直的证明方法:1、线线垂直⇒线面垂直;2、面面垂直⇒线面垂直;3、![]() ⇒线面垂直.
⇒线面垂直.

练习册系列答案
相关题目
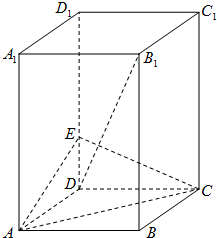 (2012•广州一模)如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点.
(2012•广州一模)如图,长方体ABCD-A1B1C1D1中,底面ABCD是正方形,AA1=2AB=2,E是DD1上的一点. 如图正六边形ABCDEF中,P是△CDE内(包括边界)的动点,设
如图正六边形ABCDEF中,P是△CDE内(包括边界)的动点,设 (2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量
(2013•资阳模拟)如图,在边长为2的正六边形ABCDEF中,P是△CDE内(含边界)的动点,设向量 (2011•温州二模)如图,在多面体ABCDE中,四边形ABCD是正方形,AE⊥平面CDE,垂足为E,AE=3,CE=9,
(2011•温州二模)如图,在多面体ABCDE中,四边形ABCD是正方形,AE⊥平面CDE,垂足为E,AE=3,CE=9,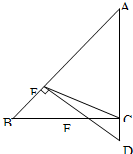 (2004•上海模拟)如图,在△ABC中,∠C=90°,sinB=
(2004•上海模拟)如图,在△ABC中,∠C=90°,sinB=