题目内容
(本小题满分12分)
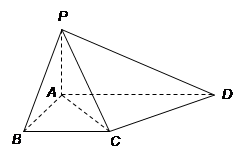
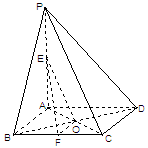
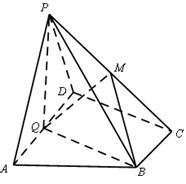
如图,在三棱锥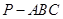 中,
中, ,
,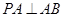 ,
,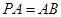 ,
,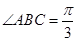 ,
,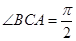 , 点
, 点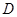 ,
, 分别在棱
分别在棱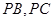 上,且
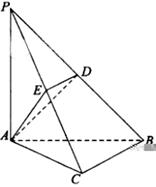
上,且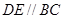 ,
,
(Ⅰ)求证: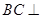 平面PAC
平面PAC
(Ⅱ)当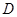 为
为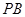 的中点时,求
的中点时,求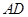 与平面
与平面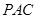 所成的角的正弦值;
所成的角的正弦值;
(Ⅲ)是否存在点 使得二面角
使得二面角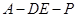 为直二面角?并说明理由.
为直二面角?并说明理由.
如图,在三棱锥
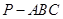 中,
中, ,
,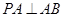 ,
,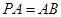 ,
,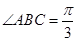 ,
,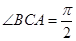 , 点
, 点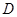 ,
, 分别在棱
分别在棱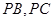 上,且
上,且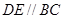 ,
,
(Ⅰ)求证:
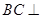 平面PAC
平面PAC(Ⅱ)当
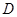 为
为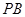 的中点时,求
的中点时,求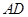 与平面
与平面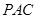 所成的角的正弦值;
所成的角的正弦值;(Ⅲ)是否存在点
 使得二面角
使得二面角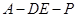 为直二面角?并说明理由.
为直二面角?并说明理由.(1)要证明线面垂直,一般可以通过线线垂直来证明,也可以通过面面垂直来证明,该试题的关键是证明AC⊥BC (2)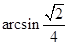
(3) 存在点E使得二面角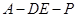 是直二面角
是直二面角
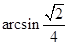
(3) 存在点E使得二面角
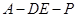 是直二面角
是直二面角试题分析:解:(法1)(Ⅰ)∵
 ,
,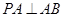 ,
,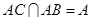 ,∴PA⊥底面ABC,∴PA⊥BC.又
,∴PA⊥底面ABC,∴PA⊥BC.又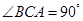 ,∴AC⊥BC.∴BC⊥平面PAC.
,∴AC⊥BC.∴BC⊥平面PAC.(Ⅱ)∵D为PB的中点,DE//BC,∴
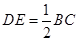 ,
,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,∵PA⊥底面ABC,
∴PA⊥AB,又PA=AB,∴△ABP为等腰直角三角形,
∴
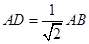 ,∴在Rt△ABC中,
,∴在Rt△ABC中,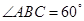 ,∴
,∴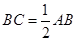 .
.∴在Rt△ADE中,
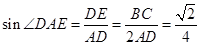 ,
,∴
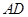 与平面
与平面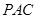 所成的角的大小
所成的角的大小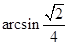 .
.(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE
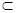 平面PAC,PE
平面PAC,PE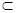 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角
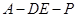 的平面角,∵PA⊥底面ABC,
的平面角,∵PA⊥底面ABC,∴PA⊥AC,∴
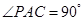 .∴在棱PC上存在一点E,使得AE⊥PC,
.∴在棱PC上存在一点E,使得AE⊥PC,这时
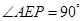 ,故存在点E使得二面角
,故存在点E使得二面角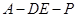 是直二面角.
是直二面角.(法2)如图,以A为原煤点建立空间直角坐标系
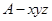 ,设
,设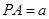 ,
,由已知可得
 ,
,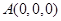 ,
,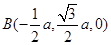 ,
,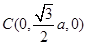 .
.(Ⅰ)∵
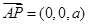 ,
,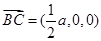 ,∴
,∴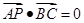 ,
,∴BC⊥AP.又∵
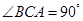 ,∴BC⊥AC,∴BC⊥平面PAC.
,∴BC⊥AC,∴BC⊥平面PAC.(Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴
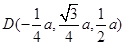 ,
,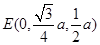 ,∴又由(Ⅰ)知,BC⊥平面PAC,
,∴又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,垂足为点E.∴∠DAE是AD与平面PAC所成的角,
∵
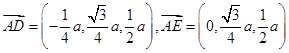 ,
,∴
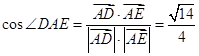 ,
,∴
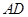 与平面
与平面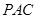 所成的角的大小
所成的角的大小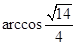 。
。(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE
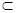 平面PAC,PE
平面PAC,PE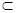 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角
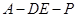 的平面角,∵PA⊥底面ABC,
的平面角,∵PA⊥底面ABC,∴PA⊥AC,∴
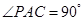 .∴在棱PC上存在一点E,
.∴在棱PC上存在一点E,使得AE⊥PC,这时
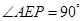 ,
,故存在点E使得二面角
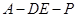 是直二面角.
是直二面角.点评:解决的关键是利用已知中的线线垂直来证明线面垂直,同时得到线面角的大小,结合三角形求解,同时要结合三垂线定理得到二面角的大小,属于基础题。

练习册系列答案
相关题目
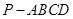 中,底面
中,底面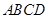 为直角梯形,且
为直角梯形,且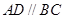 ,
,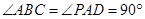 ,侧面
,侧面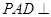 底面
底面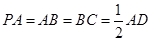 .
.
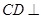 平面
平面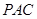 ;
;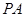 上是否存在点
上是否存在点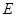 ,使得
,使得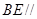 平面
平面 ?若存在,指出点
?若存在,指出点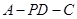 的余弦值.
的余弦值. 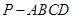 中,
中,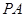 ⊥平面
⊥平面 ,
,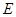 为
为 为
为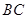 的中点,底面
的中点,底面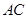 ,
, 交于点
交于点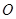 .
.
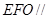 平面
平面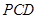 ;
; ⊥平面
⊥平面 .
.
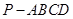 中,平面
中,平面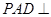 平面
平面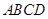 ,
,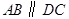 ,
,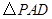 是等边三角形,已知
是等边三角形,已知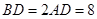 ,
,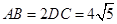 .
.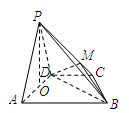
 是
是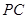 上的一点,证明:平面
上的一点,证明:平面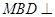 平面
平面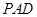 ;
;
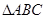 中,
中,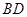 为
为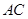 边上的高,
边上的高, ,沿
,沿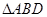 翻折,使得
翻折,使得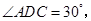 得几何体
得几何体

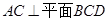 ;
; AD=1,CD=
AD=1,CD=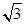 .
.
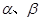 表示两个互相垂直的平面,
表示两个互相垂直的平面,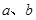 表示一对异面直线,则
表示一对异面直线,则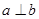 的一个充分条件是( )
的一个充分条件是( )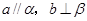 B.
B.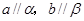
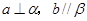 D.
D.