题目内容
数列 的前
的前 项和记作
项和记作 ,满足
,满足 ,
, .
.
 求出数列
求出数列 的通项公式.
的通项公式.
(2) ,且
,且 对正整数
对正整数 恒成立,求
恒成立,求 的范围;
的范围;
(3)(原创)若 中存在一些项成等差数列,则称
中存在一些项成等差数列,则称 有等差子数列,若
有等差子数列,若 证明:
证明: 中不可能有等差子数列(已知
中不可能有等差子数列(已知 。
。
 的前
的前 项和记作
项和记作 ,满足
,满足 ,
, .
. 求出数列
求出数列 的通项公式.
的通项公式.(2)
 ,且
,且 对正整数
对正整数 恒成立,求
恒成立,求 的范围;
的范围;(3)(原创)若
 中存在一些项成等差数列,则称
中存在一些项成等差数列,则称 有等差子数列,若
有等差子数列,若 证明:
证明: 中不可能有等差子数列(已知
中不可能有等差子数列(已知 。
。(1)
 (2)
(2) (3)不可能
(3)不可能

 (2)
(2) (3)不可能
(3)不可能(1):
 (
( )
)
作差得到: 即
即
所以 且
且 ,
,
所以
所以

(2):
令

则
 =
= +
+ -
-
=

 的最大值为
的最大值为 =1
=1
即


3:证明:因为 是递增数列,
是递增数列,
考察: =
=

假设存在 ,使得
,使得 成等差
成等差
则 ,且
,且
又因为 ,则
,则
 ,矛盾
,矛盾
故: 中不可能有某三项成等差数列
中不可能有某三项成等差数列
 中不可能有等差子数列
中不可能有等差子数列

 (
( )
)作差得到:
 即
即
所以
 且
且 ,
,所以

所以


(2):

令


则

 =
= +
+ -
-
=


 的最大值为
的最大值为 =1
=1即



3:证明:因为
 是递增数列,
是递增数列,考察:
 =
=

假设存在
 ,使得
,使得 成等差
成等差则
 ,且
,且
又因为
 ,则
,则
 ,矛盾
,矛盾故:
 中不可能有某三项成等差数列
中不可能有某三项成等差数列 中不可能有等差子数列
中不可能有等差子数列
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
 (
( 、
、 为实常数),已知不等式
为实常数),已知不等式
 均成立.定义数列
均成立.定义数列 和
和 :
:
 =
= 数列
数列 项和
项和 .
.

 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈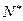 .
.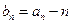 ,求数列
,求数列 的通项公式;
的通项公式;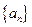 的各项均为正数,观察下面程序框图,当
的各项均为正数,观察下面程序框图,当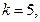
 时,分别
时,分别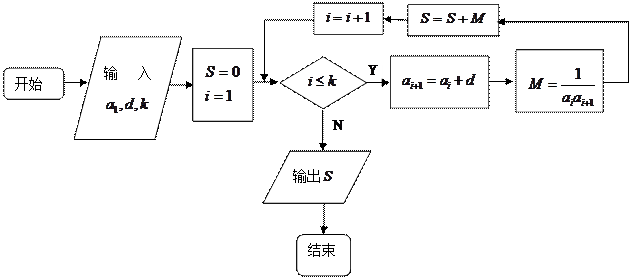
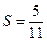 和
和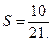 .
.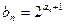 ,
,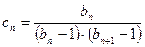
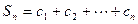 求证:
求证: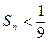 .
.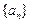 满足:
满足: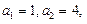 且对任意的
且对任意的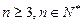 有
有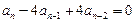 .
.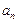 ;
;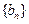 ,使得对任意的
,使得对任意的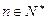 有
有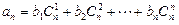 成立?证明你的结论
成立?证明你的结论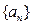 的前n项和
的前n项和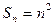 ,
, 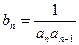 ,求数列
,求数列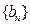 的前n项和
的前n项和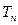 .
.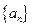 的前
的前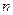 和为
和为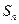 ,且有
,且有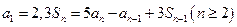
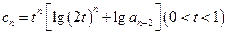 ,且数列
,且数列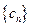 中的每一项总小于它后面的项,求实数
中的每一项总小于它后面的项,求实数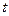 的取值范围。
的取值范围。