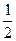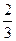题目内容
设函数 (
( 、
、 为实常数),已知不等式
为实常数),已知不等式
对任意的实数 均成立.定义数列
均成立.定义数列 和
和 :
:
 =
=
 数列
数列 的前
的前 项和
项和 .
.
(I)求 、
、 的值;
的值;
(II)求证:
(III)求证:
 (
( 、
、 为实常数),已知不等式
为实常数),已知不等式
对任意的实数
 均成立.定义数列
均成立.定义数列 和
和 :
:
 =
= 数列
数列 的前
的前 项和
项和 .
.(I)求
 、
、 的值;
的值;(II)求证:

(III)求证:

(1) a="2" b=-3(2)同解析 (3)同解析
(I)由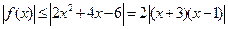 得
得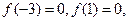
故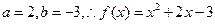
(II)由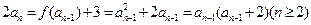 得
得
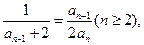
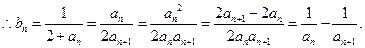
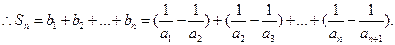
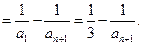
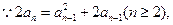
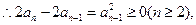
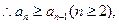
从而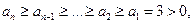 即
即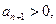
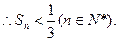
(III)由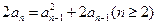 得
得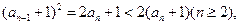
设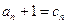 ,则
,则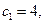 且
且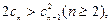
于是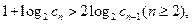
设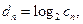 则
则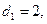 且
且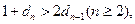
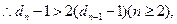
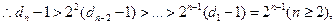
从而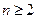 时,
时,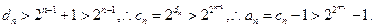
当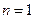 时,
时,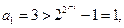
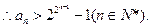
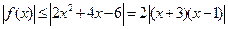 得
得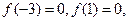
故
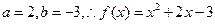
(II)由
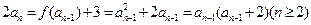 得
得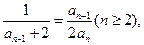
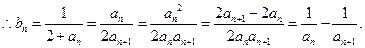
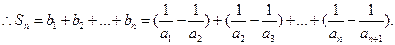
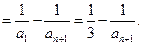
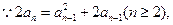
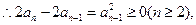
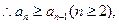
从而
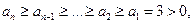 即
即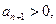
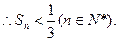
(III)由
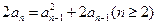 得
得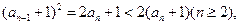
设
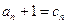 ,则
,则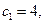 且
且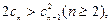
于是
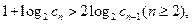
设
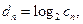 则
则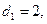 且
且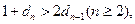
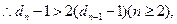
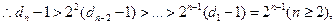
从而
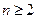 时,
时,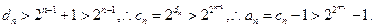
当
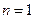 时,
时,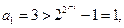

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 过曲线
过曲线 上一点
上一点 ,斜率为
,斜率为 ,且
,且 ,其中
,其中
 表示
表示 ;
; ;
;  对
对 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。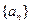 的前
的前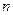 项和为
项和为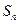 ,已知
,已知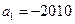 ,
,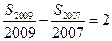 ,则
,则 ()
()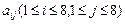 中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且
中,i表示该数所在的行数,j表示该数所在的列数。已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且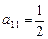 ,
,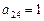 ,
,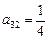 。
。  ,求
,求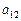 和
和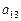 的值。
的值。 ,联
,联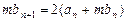 (m为非零常数),
(m为非零常数), ,且
,且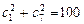 ,求
,求 的取值范围。
的取值范围。 ,记
,记 ,设
,设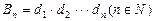 ,求数列
,求数列 中最大项的项数。
中最大项的项数。 的前
的前 项和记作
项和记作 ,满足
,满足 ,
, .
. 求出数列
求出数列 ,且
,且 对正整数
对正整数 的范围;
的范围; 证明:
证明: 中不可能有等差子数列(已知
中不可能有等差子数列(已知 。
。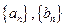
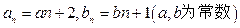
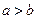
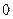 个
个 个
个 个
个 }为等差数列,则a11等于( )
}为等差数列,则a11等于( )